Неоднородные системы

Рассмотрим произвольную СЛАУ Ax = b. Заменив столбец b свободных членов нулевым, получим однородную СЛАУ Ax = 0, соответствующую неоднородной СЛАУ Ax = b. Справедливо следующее утверждение о структуре произвольного решения неоднородной СЛАУ.

Теорема 14.4. Пусть столбец x° — некоторое решение СЛАУ Ax = b. Произвольный столбец x является решением этой СЛАУ тогда и только тогда, когда он имеет представление x = x° + у, где y — решение соответствующей однородной СЛАУ Ay = 0.

◄ Если x — решение СЛАУ Ax = b, то A(x — x°) = Ax — Ax° = b — b = 0. Поэтому столбец y = x — x° является решением соответствующей однородной СЛАУ, и мы получаем представление x = x° + y.

Наоборот, если y — произвольное решение соответствующей однородной системы, то x = x° + y — решение системы Ax = b, так как A(x° + y) = Ax° + Ay = b + 0 = b. ►

Следствие 14.3. Пусть x' и x'' — решения неоднородной системы Ax = b. Тогда их разность y = x' — x'' является решением соответствующей однородной системы Ay = 0.

Теорема 14.4 сводит проблему решения СЛАУ к случаю однородной системы: чтобы описать все решения неоднородной СЛАУ, достаточно знать одно ее решение (частное решение) и все решения соответствующей однородной СЛАУ.

Чтобы решить неоднородную систему, надо, во-первых, убедиться, что она совместна (на-пример, по теореме 13.1 Кронекера — Капелли), а во-вторых, найти частное решение x° этой системы, чтобы свести ее к однородной системе.

Следствием теорем 14.3 и 14.4 является теорема о структуре общего решения неоднородной СЛАУ.

Теорема 14.5. Пусть x° — частное решение СЛАУ Ax = b и известна фундаментальная система решений x(¹), ..., x(^k) соответствующей однородной системы Ax = 0. Тогда любое решение СЛАУ Ax = b можно представить в виде

x = x° + c₁x(¹) + c₂x(²) + ... + c_kx(^k), (14.8)

где c_i ∈ R, i = 1,k. #

Как и в случае однородной СЛАУ, название теоремы отражает то, что формула

x = x° + x_oo, x_oo = c₁x(¹) + ... + c_kx(^k), (14.9)

при произвольных постоянных c_i ∈ R, i = 1,k, описывает все множество решений СЛАУ Ax = b. Формулу (14.9) называют общим решением СЛАУ.

Как найти частное решение неоднородной СЛАУ Ax = b? Пусть для соответствующей однородной системы Ax = 0 выбраны базисные и свободные неизвестные. Базисный минор матрицы A является базисным и для расширенной матрицы (A | b), если СЛАУ Ax = b совместна.

Поэтому строки базисного минора определяют те уравнения СЛАУ Ax = b, из которых следуют остальные. Эти остальные можно отбросить. Итак, пусть есть СЛАУ

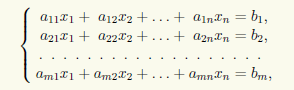
и базисный минор матрицы СЛАУ сосредоточен вверху слева:

Тогда исходная система эквивалентна следующей:

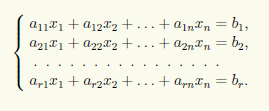
Зададим нулевые значения x_r+1 = ... = x_n = 0 для свободных неизвестных и получим СЛАУ с невырожденной матрицей

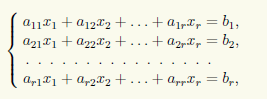
имеющей единственное решение. Решая последнюю систему, находим значения x°₁, ..., x°_r. Тогда частным решением будет столбец (x°₁, ..., x°_r, 0, ..., 0)^T .