Линейные операции над матрицами
ТеорияПрежде чем обсуждать какие бы то ни было операции над матрицами, договоримся, какие матрицы мы будем считать равными.
Определение 10.2. Две матрицы называют равными, если они имеют один и тот же типo и если у них совпадают соответствующие элементы.
Определение 10.3. Суммой матриц A = (аij) и B = (bij) типа m×n называют матрицу C = (cij) того же типа с элементами cij = аij + bij, i = 1, m, j = 1, n.
Для суммы матриц используют обозначение: C = A + B. В подробной записи
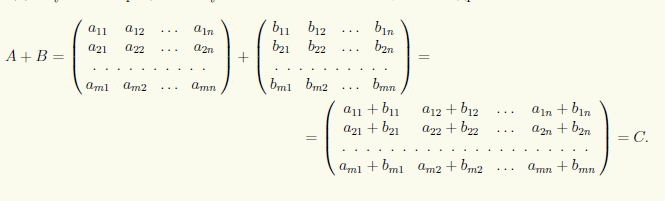
Замечание 10.1. Сумма определена только для матриц одного типа.
Пример 10.1. Найдем сумму двух матриц

Определение 10.4. Произведением матрицы A = (aij) типа m×n на число α ∈ R называют матрицу C = (cij) типа m×n с элементами cij = αaij
Подробно это произведение выглядит так:
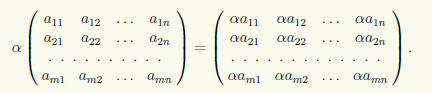
Замечание 10.2. Операции сложения и умножения на число для матриц аналогичны одноименным операциям над векторами. Эти операции также называют линейными.
Для любых матриц A = (aij), B = (bij) и C = (cij) из Mmn(R) ,верны следующие свойства линейных операций.
1°. Сложение матриц коммутативно: А + В = В + А.
◄ Доказательства равенств матриц часто проводят, основываясь на определении 10.2, т.е. доказывают, что матрицы, стоящие в левой и правой частях равенства, имеют на одинаковых местах равные элементы. Так, свойство коммутативности суммы матриц следует из равенств
[А + В ]ij = aij + bij = bij + aij = [В + A]ij,
среди которых первое и третье следуют из определения 10.3 суммы двух матриц, а второе верно в силу коммутативности сложения действительных чисел. ►
2°. Сложение матриц ассоциативно: (А + В) + С = А + (В + С).
◄ Как и в случае коммутативности, свойство ассоциативности вытекает из равенств
[(А + В) + С ]ij = [А + В ]ij + [С ]ij = (aij + bij) + cij = aij + (bij + cij) = [ А]ij + [В + С ]ij = [А + (В + С )]ij,
которые имеют место в силу определения 10.3 суммы двух матриц и ассоциативности сложения действительных чисел. ►
Свойства 1° и 2° позволяют не заботиться о порядке операций сложения матриц и порядке слагаемых в матричных выражениях.
3°. Существует такая матрица O ∈ Mmn(R), что для любой матрицы A ∈ Mmn(R) выполнено равенство А + O = А.
◄ Матрица O — это нулевая матрица Θ типа m×n. Действительно, [A + Θ]ij = [A]ij + [Θ]ij = aij + 0 = aij = [A]ij. ►
4°. Для любой матрицы A ∈ Mmn(R) существует такая единственная матрица B ∈ Mmn(R), для которой выполнено равенство A + B = Θ, где Θ — нулевая матрица.
◄ Если A + B = Θ, то [A + B]ij = aij + bij = [ Θ]ij = 0 и, следовательно, aij + bij = 0. Значит, элементами bij матрицы B являются bij = — aij, и это доказывает как единственность, так и существование матрицы B. ►
Матрицу B, о которой говорится в свойстве 4°, называют противоположной A и обозначают через — A. Эта матрица получается из матрицы А умножением на число —1.
Свойства 3° и 4° позволяют ввести операцию вычитания матриц. Разностью P — Q матриц P и Q одного типа называют матрицу P + (—Q).
5°. Умножение матрицы на число ассоциативно: (λμ)A = λ(μA).
◄ [(λμ)A]ij = (λμ)аij = λ(μаij) = λ[μA]ij ►
6°. Умножение матрицы на число дистрибутивно относительно суммы действительных чисел: (λ + μ)A = λA + μA.
◄ [(λ + μ)A]ij = (λ + μ)аij = λaij + μаij = [λA]ij + [μA]ij = [λA + μA]ij. ►
7°. Умножение матрицы на число дистрибутивно относительно суммы матриц: λ(A + В) = λA + λВ.
◄ [λ(A + B )]ij = λ[A + B ]ij = λ(aij + bij) = λaij + λbij = [λA]ij + [λB]ij = [λA + λB]ij. ►
8°. Умножение матрицы на 1 не меняет ее: 1 • А = А.
◄ [1 • А]ij = 1 • [А]ij = [А]ij ►