Блочные матрицы
ТеорияЕсли разделить некоторую матрицу А на части вертикальными и горизонтальными прямыми, то получаются прямоугольные ячейки, являющиеся сами по себе матрицами. Эти ячейки называют блоками матрицы. Сама матрица А может рассматриваться как таблица, элементами которой являются более мелкие матрицы Mαβ: А = (Mαβ). При таком построении матрица А составляется из блоков, и поэтому ее называют блочной. Например, матрицу А разобьем на блоки
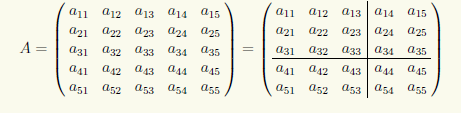
и обозначим их
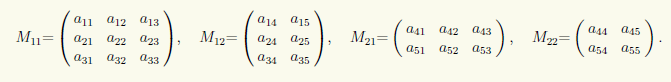
Тогда матрицу А можно записать в виде блочной матрицы, элементами которой будут эти матрицы
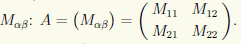
Для составления блочной матрицы из серии матриц Mαβ необходимо, чтобы подмножества матриц из серии с одинаковым значением индекса α имели одинаковое количество строк, а под-множества матриц с одинаковым значением индекса β — одинаковое количество столбцов. Эти подмножества образуют соответственно " блочные " строки и " блочные " столбцы (соответству-ющие нескольким строкам или столбцам обычной записи матрицы).
Пример 10.11. Указанным требованиям удовлетворяют следующие четыре матрицы:
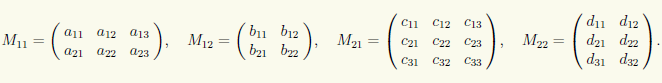
Поэтому из них можно составить блочную матрицу
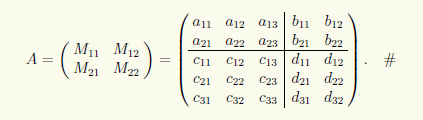
Основное свойство блочных матриц состоит в том, что операции над блочными матрицами совершаются по тем же правилам, что и операции над обычными матрицами. В самом деле, это в достаточной степени очевидно для суммы матриц и произведения матрицы на число. Однако относительно суммы это можно утверждать лишь в том случае, когда размеры слагаемых блочных матриц, равно как и размеры отдельных блоков с равными индексами у слагаемых, совпадают.
Подробнее рассмотрим ситуацию с умножением блочных матриц. Пусть блочные матрицы А = (Аαβ) и В = (Bβγ) удовлетворяют двум условиям.
1. Число "блочных" столбцов матрицы А совпадает с числом "блочных " строк матрицы B (т.е. индекс β для А и B изменяется в одинаковых пределах).
2. Для любых индексов α, β, γ число столбцов у матрицы Aαβ совпадает с числом строк у матрицы Bβγ.
Тогда AB = (Cαγ), Cαγ = ΣβАαβВβγ. Для доказательства этого равенства достаточно расписать обе его части через элементы матриц.
Указанные два условия довольно сложны, но все упрощается, если блоки матриц — это квадратные матрицы одного порядка. В этом случае условия близки к обычным: число " блочных " столбцов множимого должно совпадать с числом " блочных " строк множителя.
Представление матриц в блочном виде часто оказывается удобным при нахождении суммы и произведения, если матрицы имеют достаточно большие размеры, а их согласованные разбиения на блоки содержат нулевые, единичные, диагональные, треугольные матрицы.
Пример 10.12. Найдем произведения следующих блочных матриц предполагая, что все операции определены:
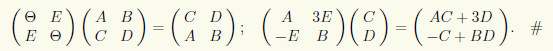
При транспонировании блочной матрицы транспонированию подлежат и ее элементы. Например,
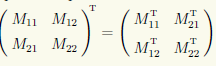
Пример 10.13. Транспонируем блочную матрицу: