Конусы

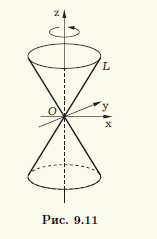
При вращении прямой L, пересекающейся с осью вращения, образуется прямой круговой конус (рис. 9.11). Точка пересечения вращающейся прямой с осью вращения остается неподвижной, ее называют вершиной конуса .

Как и ранее, уравнение будем выводить в прямоугольной системе координат, ось Oz которой совпадает с осью вращения, а начало системы координат — с вершиной конуса. Ось Ox расположим так, чтобы прямая L находилась в координатной плоскости xOz и описывалась уравнением z = k₁x. В этой системе координат уравнение поверхности вращения получается из уравнения прямой заменой x на ±√(х² + у²) (см. 9.1). В результате такой замены получаем z = ±k₁√(х² + у²). Возведя уравнение в квадрат, придем к соотношению z² = k²₁(x² + у²), а разделив его на с² = k²₁a², получим каноническое уравнение прямого кругового конуса x²/a² + y²/a^{2 + z2/c2}

Преобразование сжатия прямого кругового конуса к координатной плоскости xOz с коэффициентом k дает эллиптический конус. Его уравнение имеет вид x²/a² + k²y²/b² = z²/c² после переобозначения параметров,

x²/a² + k²y²/b² = z²/c² (9.9)

Уравнение называют каноническим уравнением эллиптического конуса. Эллиптический конус при а = b совпадает с прямым круговым конусом, и оба они являются поверхностями второго порядка.