Специальные виды уравнения прямой
ТеорияКроме общего уравнения прямой на плоскости часто используют и другие уравнения прямой. Это связано с тем, что, в зависимости от геометрического описания прямой на плоскости, ее уравнение может быть получено в некотором специальном виде. Кроме того, каждому виду уравнения соответствует свой геометрический смысл его коэффициентов, что также важно. Фиксируем на плоскости прямоугольную систему координат Oxy.
Уравнение с угловым коэффициентом. Определим прямую L на плоскости, задав точку M0(x0; у0) на этой прямой и угол φ, на который надо повернуть против хода часовой стрелки ось абсцисс Ox до совмещения с прямой (рис. 4.6). Предположим, что φ ≠ π/2.
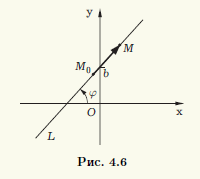
Точка M(x; у) принадлежит прямой L тогда и только тогда, когда вектор M0M составляет с осью Ox угол φ или π — φ, при этом отношение координат этого вектора равно tg φ. Это условие можно записать в виде (y-y0)/ (x-x0) = tgφ. Находя у, приходим к уравнению
у = kx + b, (4.17)
где k = tgφ; b = у0 — x0tgφ.
Уравнение вида у = kx + b называют уравнением прямой с угловым коэффициентом. Параметр k (угловой коэффициент прямой) равен тангенсу угла наклона прямой. Параметр b равен ординате точки пересечения прямой с осью Oy.
Векторное и параметрические уравнения прямой. Определим прямую L на плоскости точкой M0(x0; у0) на этой прямой и ненулевым вектором s = {l; m}, параллельным ей (рис. 4.7). Такой вектор s называют направляющим вектором прямой L.
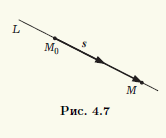
Если точка M(x; у) принадлежит прямой L, то это эквивалентно тому, что вектор M0M коллинеарен вектору s, т.е. эти векторы принадлежат одному и тому же пространству V1. Так как вектор s не равен нулевому, он образует базис в этом пространстве V1. Следовательно, для некоторого числа t выполняется равенство M0M = ts. Воспользовавшись тем, что M0M = {x — x0; у — у0}, s = {l; m}, запишем это равенство в координатах:
x — x0 = lt, у — у0 = mt,
или
x = x0 + lt, у = у0 + mt. (4.18)
Уравнения (4.18) называют параметрическими уравнениями прямой. Точка M(x0; у0), лежащая на прямой, соответствует значению параметра t = 0.
Если равенство M0M = ts записать через радиус-векторы r0 и r точек M0 и M соответственно, то в результате получим векторное уравнение прямой
r — r0 = ts, или r = r0 + ts. (4.19)
Каноническое уравнение прямой. Модифицируем вывод параметрических уравнений прямой. Коллинеарность векторов M0M и s, согласно следствию 2.1, эквивалентна равенству отношений их одноименных координат:
(x - x0)/l = (y - y0)/m (4.20)
Уравнение (4.20) называют каноническим уравнением прямой. Это уравнение можно также получить, исключив из параметрических уравнений (4.18) параметр t.
Уравнение прямой, проходящей через две точки. Зададим прямую L на плоскости двумя различными точками M1(x1,y1) и M2(x2,y2) на ней.
Тогда вектор M1M2 параллелен L и ее каноническое уравнение (4.20) как уравнение прямой, проходящей через точку M1(x1,y1), с направляющим вектором s = M1M2, имеет вид
(x - x1)/(x1 - x1) = (y - y1)/(y1 - y1) (4.21)
Уравнение (4.21) называют уравнением прямой, проходящей через две точки.
Уравнение прямой в отрезках. Определим прямую L ее точками A(a, 0) и B(0,b) пересечения с осями координат, предполагая, что эти две точки не совпадают с началом системы координат, т.е. что a ≠ 0 и b ≠ 0 (рис. 4.8).
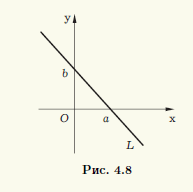
Записывая уравнение прямой L в виде (4.21) по двум ее точкам A и B, получаем (x - a)/(0 - a) = (y - 0)/(b - 0), откуда — x/a + 1 = y/b, или
x/a + y/b = 1. (4.22)
Уравнение прямой (4.22) называют уравнением прямой в отрезках.
Нормальное уравнение прямой. Определим прямую L при помощи перпендикулярного ей единичного вектора n и расстояния p > 0 до прямой от начала системы координат. Существуют два единичных вектора, перпендикулярных прямой L. Из этих двух выберем тот, который имеет начало в точке O и направлен "в сторону прямой" L (рис. 4.9).
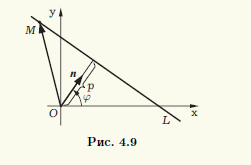
Выбранный вектор n однозначно определяется своим углом φ с осью Ox, который отсчитывается против хода часовой стрелки. Координаты вектора n легко вычисляются через этот угол: n = {cosφ; sinφ}.
Условие, что точка M(x; у) принадлежит прямой L, эквивалентно тому, что ортогональная проекция радиус-вектора точки M на направление нормального вектора прямой равна расстоянию p от точки O до прямой: прn OM = p (см. рис. 4.9). Проекция прn OM совпадает со скалярным произведением векторов OM и n, так как длина нормального вектора n равна единице, и это приводит к равенству OMn = p. Записав скалярное произведение OMn в координатах, получим уравнение прямой L в виде
xcosφ + уsinφ — p = 0. (4.23)
Уравнение (4.23) называют нормальным уравнением прямой. Параметрами в этом уравнении являются угол φ между нормальным вектором прямой и осью Ox и расстояние от начала системы координат до прямой.
Общее уравнение прямой ax + by + с = 0 можно преобразовать в ее нормальное уравнение делением на нормирующий множитель ± √(a2 + b2), знак которого выбирается противоположным знаку c. По абсолютной величине нормирующий множитель представляет собой длину нор-мального вектора {a; b} прямой, а выбор знака означает выбор нужного направления из двух возможных. Если с = 0, то прямая проходит через начало координат (p = 0). В этом случае знак нормирующего множителя можно выбирать любым.
Пример 4.7. Для получения нормального уравнения прямой из ее общего уравнения 3x — 4у + 10 = 0 вычисляем нормирующий множитель ±√(a2 + b2), который для данной прямой отрицателен и равен — √(32 + 42) = — 5. Поэтому нормальное уравнение прямой имеет вид
- 3/5x + 4/5y - 2 = 0
В данном случае имеем p = 2, cosφ = — 3/5, sinφ = 4/5, а φ = arccos(—3/5).