Вычисления в координатах
ТеорияВыясним, что происходит с координатами векторов при выполнении линейных операций.
Теорема 2.5. При сложении двух векторов их координаты в одном и том же базисе складываются. При умножении вектора на число координаты этого вектора умножаются на это число.
◄ Для простоты остановимся, например, на пространстве V3. Фиксируем в V3 базис e1, е2, е3. Возьмем два произвольных вектора x и у и запишем их разложения в выбранном базисе: x = x1e1 + x2e2 + x3e3, у = y1e1 + y2e2 + y3e3. Используя свойства линейных операций, вычисляем сумму этих векторов:
x + у = (x1e1 + x2e2 + x3e3) + (y1e1 + y2e2 + y3e3) = (x1 + y1)e1 + (x2 + y2)е2 + (x3 + y3)е3.
Мы получили разложение суммы векторов в фиксированном базисе. Отсюда заключаем, что координаты xi и уi исходных слагаемых, соответствующие одному вектору еi в базисе (i = 1, 2, 3), складываются.
Аналогично с учетом свойств линейных операций имеем λx = λ(x1e1 + x2е2 + x3e3) = (λx1)e1 + (λx2)e2 + (λx3)e3. В итоге получаем разложение вектора λx в фиксированном базисе. Из этого разложения видим, что каждая из координат исходного вектора x умножена на число λ. ►
Разложение вектора в базисе имеет простой геометрический смысл. Рассмотрим, например, пространство V3. Разложение вектора d в базисе, скажем a, b, с, показано на рис. 2.2. Координатами вектора d будут отношения
da = ± |OA'|/|OA|, db = ± |OB'|/|OB|, dc = ± |OC'|/|OC|,
где знаки выбирают в зависимости от того, является соответствующая пара коллинеарных векторов (например, OA и OA' для da) однонаправленной или нет.
Теорема 2.6. Для того чтобы два вектора были коллинеарны, необходимо и достаточно, чтобы их одноименные координаты в одном и том же базисе были пропорциональны.
◄ Докажем теорему в случае пространства V3. Фиксируем в V3 базис e1, е2, е3. Рассмотрим разложения в выбранном базисе векторов x и у:
x = x1e1 +x2e2 + x3е3, у = y1e1 + y2e2 + y3е3. (2.6)
Если одноименные координаты этих векторов пропорциональны, т.е. существует такое λ ∈ R, что выполнены равенства
x1 = λy1, x2 = λy2, x3 = λy3, (2.7)
то x = x1e1 + x2e2 + x3e3 = λy1e1 + λy2e2 + λy3e3 = λ(y1e1 + y2e2 + y3e3) = λy и из теорем 2.1, 2.2 следует, что векторы x и у коллинеарны. Достаточность условия доказана. Для доказательства его необходимости предположим, что векторы x и у коллинеарны. Но тогда по теореме 2.2 они линейно зависимы и в силу теоремы 2.1 один из них, например x, является линейной комбинацией "остальных", т.е. x = λy. Подставляя в это равенство разложения (2.6), получаем x1e1 + x2e2 + x3e3 = λ(y1e1 + y2e22 + y3e3), или (x1 - λy1)e1 + (x2 - λy2)e2 + (x3 - λy3)e3 = 0.
А поскольку вектор 0 в любом базисе имеет нулевые координаты, то из последнего равенства следуют соотношения (2.7). ►
Следствие 2.1. Для того чтобы два вектора были коллинеарны, необходимо и достаточно, чтобы отношения их одноименных координат в одном и том же базисе были равны.
◄ Выражая λ из соотношений (2.7) и приравнивая полученные дроби, находим, что
x1/y1 = x2/y2 = x3/y3 (2.8)
Отметим, что в условии (2.8) в знаменателях дробей могут стоять нули, но при этом подразумевается, что и в числителе соответствующей дроби стоит нуль. Для пространства V2 условие (2.8) сводится к равенству только первых двух дробей. ►
Пример 2.1. Пусть векторы e1, е2 образуют базис в V2. Векторы a = 2e1 - 3е2, b = -e1 + 3е2 линейно независимы, так как 2/(-1) ≠ -3/3. Поэтому они тоже образуют базис в пространстве V2. Найдем разложение в этом базисе векторов e1 и с = 3e1 - 6е2.
Чтобы найти разложение вектора e1, вычислим сумму векторов a и b: a + b = e1. Следовательно, искомым разложением является e1 = a + b.
Чтобы найти разложение вектора с, поступим следующим образом. Пусть с = λ1a + λ2b. Подставив в это равенство разложения векторов с, a, b в базисе e1, е2, приведем подобные слагаемые в правой части равенства. Получим, что
3e1 - 6е2 = λ1(2e1 - 3е2) + λ2(-e1 + 3е2) = (2λ1 - λ2)e1 + (-3λ1 + 3λ2)e2.
Поскольку каждый вектор в любом базисе имеет единственное разложение, то λ1, λ 2должны удовлетворять системе уравнений
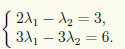
Решая эту систему, находим, что λ1 = 1, λ2 = -1. Это значит, что с = a - b.
Определение 2.2. Базис называют ортогональным, если он состоит из векторов, лежащих на взаимно перпендикулярных прямых. Базис называют ортонормированным, если он ортогональный и состоит из единичных векторов.
Параллелепипед, изображенный на рис. 2.2 в ортонормированном базисе i, j, k в V3, является прямоугольным, а точки A', B', С' - ортогональными проекциями точки D на соответствующие прямые. Координаты вектора d = OD в ортонормированном базисе равны ортогональным проекциям этого вектора на направления векторов, образующих этот базис.
Ортонормированный базис в пространстве V3 принято обозначать, с учетом порядка, буквами i, j, k, в V2 - соответственно i, j и в V1 - i.
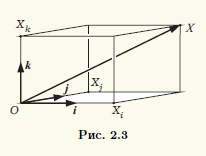
В случае ортонормированного базиса в пространстве V3 легко найти расстояние от точки O до произвольной точки X. По теореме Пифагора |OX|2 = |OXi|2 + |OXj|2 + |OXk|2 (рис. 2.3), где точки Xi, Xj, Xk - ортогональные проекции точки X на соответствующие оси. Но длины отрезков OXi, OXj, OXk - это абсолютные значения координат вектора x = OX в базисе i, j, k. В результате получаем формулу для вычисления длины вектора x с координатами {x1; x2; x3} в ортонормированном базисе i, j, k пространства V3:
|x| = √(x21 + x22 + x23), x ∈ V3. (2.9)
Аналогично вычисляют длину вектора из пространства V2 по его координатам x1, x2 в ортонормированном базисе:
|x| = √(x21 + x22 ), x ∈ V2. (2.10)
и длину вектора из V1 с координатой x1 в ортонормированном базисе:
|x| = √(x21 ) = |x1|, x ∈ V1. (2.10)
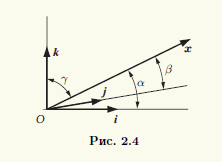
Пусть ненулевой вектор x ∈ V3 образует с направлениями векторов ортонормированного базиса i, j, k углы α, β и γ соответственно. Величины cosα,cosβ, cosγ называют направляющими косинусами вектора x (рис. 2.4). Направляющие косинусы не зависят от длины вектора, они характеризуют направление вектора и при умножении вектора на положительное число не изменяются.
Направляющие косинусы вектора можно использовать при вычислении его координат. Если ненулевой вектор x ∈ V3 имеет в ортонормированном базисе i, j, k координаты {x1; x2; x3} и направляющие косинусы cosα,cosβ, cosγ, то
x1 = |x|cosα, x2 = |x|cosβ, x3 = |x|cosγ. (2.12)
Используя формулу (2.9) для вычисления длины вектора, получаем |x|2 = |x|2 cos2α + + |x|2cos2β + |x|2cos2γ, откуда после сокращения на |x| ≠ 0 вытекает следующая формула связи для направляющих косинусов:
cos2α + cos2β + cos2γ = 1. (2.13)
Для любых углов α,β, γ из отрезка [0, π], удовлетворяющих соотношению (2.13), существует вектор, направляющими косинусами которого являются величины cosα, cosβ, cosγ. В качестве примера можно взять вектор {cosα, cosβ, cosγ}. Согласно формулам (2.9) и (2.13) этот вектор имеет единичную длину, а значения cosα, cosβ, cosγ представляют собой направляющие косинусы этого вектора.
В случае ортонормированного базиса в пространстве V2 направление вектора удобно указывать одним углом φ, который отсчитывается от первого вектора базиса против хода часовой стрелки в случае положительного значения (рис. 2.5). Угол φ, длина вектора x и его координаты {x1; x2} связаны соотношениями: x1 = |x| cosφ, x2 = |x| sinφ.