Ранг системы векторов

Определение 2.5. Рангом системы векторов в линейном пространстве называют размерность линейной оболочки этой системы векторов.

Теорема 2.6. Ранг системы векторов а = (a₁ ... а_k) линейного пространства L равен:

а) максимальному количеству линейно независимых векторов в системе а;

б) рангу матрицы, составленной по столбцам из координат векторов a₁,..., a_k в каком-либо базисе линейного пространства L.

◄ Пусть g - некоторый базис в L. Составим по столбцам матрицу А из координат в базисе g векторов а_i, i = 1,k. Линейные операции над векторами а_i соответствуют таким же линейным операциям над столбцами их координат. Поэтому, согласно следствию 1.1, векторы линейно независимы тогда и только тогда, когда столбцы их координат линейно независимы. По теореме о базисном миноре [III] ранг матрицы А равен максимальному количеству ее линейно независимых столбцов. Это совпадает с максимальным количеством линейно независимых векторов в системе о. Следовательно, утверждения а) и б) теоремы эквивалентны.

Выберем в матрице А какой-либо базисный минор и зафиксируем столбцы этого минора (базисные столбцы). Соответствующие им векторы будем называть базисными. По теоремр о базисном миноре, во-первых, базисные столбцы линейно неза-висимы и поэтому базисные векторы образуют линейно незави: симую систему, а во-вторых, все остальные столбцы матрицы являются линейными комбинациями базисных и поэтому неба-зисные векторы системы выражаются через базисные. Сле-довательно, любая линейная комбинация векторов системы а сводится к линейной комбинации системы базисных векторов, т.е. любой вектор линейной оболочки системы векторов а вы-ражается через базисные векторы. Значит, базисные векторы образуют базис линейной оболочки. Количество базисных век-торов, с одной стороны, равно количеству базисных столбцов, т.е. рангу матрицы А, а с другой - совпадает с размерностью линейной оболочки, т.е. с рангом системы векторов а. ►

Замечание 2.2. Как следует из приведенного доказательства, столбцы любого базисного минора матрицы А отвечают набору векторов системы a, являющемуся базисом в span{a} - линейном подпространстве, порожденном этой системой векторов.

Пример 2.11. Пусть даны векторы a₁, a₂, а₃, а₄ в четырехмерном линейном пространстве L, имеющие в некотором базисе столбцы координат a₁ = (1 2 0 6)^T , а₂ = (2 0 3 1)^T ,а₃ = (3 2 3 7)^T , a₄ = (7 2 9 9)^T . Соответствующая матрица А имеет вид

Вычислив ранг матрицы, убеждаемся, что он равен 2. Таким образом, ранг системы векторов равен 2. Легко проверить, что любой минор второго порядка является базисным. Поэтому базисом линейной оболочки этой системы векторов будут любые два вектора системы. Например, базисом является пара векторов a₁, a₂. По этому базису можно разложить, напримep, остальные векторы системы. Чтобы найти разложение вектора а₃ по базису, достаточно решить систему линейных алгебраических уравнений

х₁а₁ + x₂a₂ = а₃

которая в координатной форме имеет вид

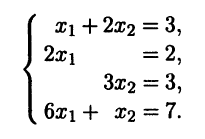
Из четырех уравнений можно оставить любые два. Используя второе и третье уравнения, находим x₁ = 1, x₂ = 1 и, следовательно, а₃ = a₁ + a₂. Аналогично находим и разложение вектора a₄: a₄ = a₁ + 3a₂.

1. Линейные операции над векторами

2. Базис. Cкалярное произведение

3. Векторное и смешанное произведения векторов

4. Декартова система координат. прямая на плоскости

5. Плоскость в пространстве

6. Прямая в пространстве

7. Кривые второго порядка — I

8. Кривые второго порядка — II

9. Поверхности второго порядка

10. Матрицы и операции с ними

11. Обратная матрица

12. Ранг матрицы

13. Системы линейных алгебраических уравнений

14. Свойства решений однородных и неоднородных СЛАУ