Собственные векторы самосопряженного оператора
Теория- Автор
- Издательство
Теорема 6.4. Собственные векторы самосопряженного оператора, отвечающие различным собственным значениям, ортогональны.
◄ Рассмотрим самосопряженный оператор А и два его собственных вектора x1 и х2, отвечающие различным собственным значениям λ1 и λ2. Тогда Ах1 = λ1x1 и Ах2 = λ2x2. Поэтому
(Ах1,x2) = (λ1x1,x2) = λ1(x1,x2) (6.6)
Но так как А является самосопряженным оператором, то (Ax1,x2) = (x1,Ax2) . Значит,
(Ax1,x2) = (x1,Ax2) = (x1, λ2x2) = λ2(x1,x2) (6.7)
Приравнивая правые части соотношений (6.6) и (6.7), получаем
λ1(x1,x2) = λ2(x1,x2)
или
(λ1 - λ2)(x1,x2) = 0. (6.8)
Так как λ1 ≠ λ2, из равенства (6.8) следует, что (x1,x2) = 0, что и означает ортогональность векторов x1 и x2. ►
Теорема 6.5. Если собственные значения λ1, ..., λn самосопряженного оператора А, действующего в n-мерном евклидовом пространстве Ε, попарно различны, то в Ε существует ортонормированный базис, в котором матрица этого линейного оператора А имеет диагональный вид, причем диагональными элементами такой матрицы являются собственные значения λ1, ..., λn.
◄ Поскольку собственные значения λ1, ..., λn попарно различны, то, выбрав для каждого λi соответствующий ему собственный вектор еi, получим систему е ненулевых векторов, которые по теореме 6.4 попарно ортогональны. Поэтому е - ортогональная система векторов. Согласно теореме 5.5, она линейно независима и, имея n векторов, является базисом (см. теорему 1.4). Этот базис является ортогональным, а чтобы его превратить в ортонормированный, необходимо каждый вектор еi нормировать делением на его длину.
Таким образом, в условиях теоремы существует базис из собственных векторов самосопряженного оператора А. По теореме 5.6 матрица линейного оператора в базисе из собственных векторов является диагональной, а диагональные элементы ма-трицы представляют собой собственные значения. ►
Хотя все корни характеристического уравнения самосопряженного оператора действительны (см. теорему 6.3), среди них могут быть кратные, и тогда теорема 6.5 неприменима. Однако и в этом случае матрица самосопряженного оператора в некотором базисе имеет диагональный вид.
Теорема 6.6. Для любого самосопряженного оператора А существует ортонормированный базис, состоящий из соб-ственных векторов этого линейного оператора. Матрица А самосопряженного оператора А в этом базисе имеет диагональный вид, на ее диагонали расположены собственные значения оператора А, повторяющиеся столько раз какова их кратность. #
Доказательство этой теоремы приведено в Д.6.1.
Следствие 6.4. Любая симметрическая матрица М порядка n подобна некоторой диагональной, т.е. существует такая невырожденная матрица Р порядка n, что
P-1MP = diag(λ1, ..., λn).
Последовательность λ1, ..., λn из n чисел представляет собой перечень всех корней характеристического уравнения матрицы М с учетом их кратностей.
◄ Рассмотрим в n-мерном евклидовом пространстве Rn стандартный ортонормированный базис, и пусть матрица М является матрицей в этом базисе некоторого линейного оператора М. Тогда этот оператор будет самосопряженным. По теореме 6.6 для него существует ортонормированный базис, в котором его матрица М' имеет диагональный вид М' = diag (λ1, ..., λ1n). Матрица М' получается из исходной матрицы М при помощи матрицы перехода Р из стандартного базиса в указанный ортонормированный базис: М' = Р-1МР. ►
Дополнение 6.1. Инвариантные подпространства самосопряженного оператора
Теорема 6.7. Если H - инвариантное подпространство самосопряженного оператора А, действующего в евклидовом пространстве Ε, то его ортогональное дополнение H⊥ - также является инвариантным подпространством этого оператора А.
◄ Нам достаточно проверить, что для любого вектора у линейного подпространства H⊥ его образ Ау тоже принадлежит H⊥, т.е. что для любого вектора х ∈ H выполнено условие (Ау, х) = 0.
Пусть у ∈ H⊥, х ∈ H. Так как оператор А самосопряженный, выполнено равенство (Ау, х) = (у, Ах). Но H - инвариантное подпространство оператора А, т.е. Ах ∈H для вектора х ∈ H. Поэтому (у, Ах) = 0, так как вектор у ∈ H⊥ ортогонален любому вектору из H, в частности вектору Ах. Следовательно, (Ау, х) = 0, что и требовалось доказать. ►
Мы видели, что кратность собственного значения и размерность соответствующего собственного подпространства линейного оператора могут не совпадать (см. пример 5.7). Эти две характеристики совпадают, если линейный оператор, действующий в евклидовом пространстве, является самосопряженным.
Теорема 6.8. Пусть λ - собственное значение самосопряженного оператора А, действующего в евклидовом пространстве Ε. Тогда кратность собственного значения λ равна размерности отвечающего этому значению собственного под-пространства £(А,λ) линейного оператора А.
◄ Собственное подпространство £(А, λ) самосопряженного оператора А является инвариантным подпространством этого оператора. Поэтому, согласно теореме 6.7, ортогональное дополнение £(А, λ)⊥ также является инвариантным подпространством самосопряженного оператора А. Пусть dim£(A, λ) = k, a dim£(A,λ)⊥ = l. Выберем в линейных подпространствах £(А,λ) и £(А,λ)⊥ базисы е = (e1 ... еk) и g = (g1 ... gl) соответственно.
Так как £(А, λ) ⊕ £(А, λ)⊥ = Ε, система векторов (е g) является базисом евклидова пространства Ε. Рассмотрим в этом базисе матрицу А оператора А. Для любого вектора еi системы е имеем Aei = λеi, так как еi принадлежит собственному подпространству £(А, λ) линейного оператора, отвечающему собственному значению λ. Для каждого вектора gj системы g имеем Agj = aj1g1 + ... + aglgl, так как £(А,λ)⊥ - инвариантное подпространство оператора А, а g - базис этого подпространства. Эти разложения означают, что матрица А оператора А в базисе (е g) имеет блочный вид:
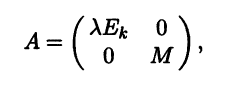
где Еk обозначает единичную матрицу порядка k, а блок М представляет собой квадратную матрицу порядка l, состоящую из коэффициентов разложения векторов Agj в базисе (е g):

Исходя из блочного представления матрицы А получаем вид ее характеристического уравнения:
ΧA( τ) = det(A - τЕn) = (λ - τ)k det(M - τЕl) = (λ - τ)kΧM(τ), (6.9)
где Еn и El - единичные матрицы порядков n и l.
Отметим, что матрица М представляет собой матрицу в базисе g линейного оператора, являющегося ограничением линейного оператора А на его инвариантное подпространство £(А,λ)⊥. Оператор А не имеет в подпространстве £(А,λ)⊥ собственных векторов с собственным значением λ. Поэтому λ не является собственным значением матрицы М, и из представления (6.9) заключаем, что собственное значение λ матрицы А имеет кратность k. ►
Доказательство теоремы 6.6 опирается на свойства инвари-антных подпространств.
◄ Пусть λ1, ..., λk - собственные значения самосопряженного оператора A, a r1, ..., rk - их кратности. Так как характеристическое уравнение самосопряженного оператора имеет только действительные корни, сумма кратностей r1 + ... + rk собственных значений равна размерности n евклидова пространства Ε. Рассмотрим собственное подпространство Hi оператора А, соответствующее собственному значению λi. Размерность этого линейного подпространства, согласно теореме 6.8, совпадает с кратностью ri собственного значения λi. Выберем ортонормированный базис в линейном подпространстве Hi, который будет состоять из ri, собственных векторов самосопряженного оператора А, попарно ортогональных и имеющих единичную длину. Объединив выбранные базисы в одну систему, получим систему из n собственных векторов единичной длины, любые два из которых ортогональны. Действительно, либо оба вектора одновременно входят в базис некоторого подпространства Hi и будут ортогональны согласно выбору, либо они попадают в разные инвариантные подпространства Hi и Hj и будут ортогональны как собственные векторы, отвечающие различным собственным значениям (см. теорему 6.4).
Итак, мы выбрали систему из п попарно ортогональных векторов единичной длины. Согласно теореме 3.4, эта система линейно независима, а так как количество векторов в ней совпадает с размерностью пространства, она является ортонормиро- ванным базисом. Согласно теореме 5.6, матрица оператора А в этом базисе является диагональной и на ее диагонали расположены собственные значения, повторяющиеся столько раз, какова их кратность, поскольку построенный базис состоит из соответствующих наборов собственных векторов. ►
Вопросы и задачи
- Известно, что матрица линейного оператора в некото-ром ортонормированном базисе диагональна. Является ли этот линейный оператор самосопряженным?
- Известно, что в некотором базисе, не являющемся ортогональным, матрица оператора А симметрическая. Можно ли утверждать, что: а) А - самосопряженный оператор; б) А не является самосопряженным оператором. Что можно утверждать, если базис ортогональный, но не ортонормированный?
- Линейный оператор, действующий в n-мерном линейном пространстве, имеет в некотором базисе симметрическую матрицу. Докажите, что этот оператор имеет базис го собственных векторов, даже если линейное пространство не является евклидовым.
- Докажите, что: а) (А + В)* = А* + В*; б) (АВ)* = В*А*; в) если линейный оператор А имеет обратный, то и оператор А* имеет обратный, причем (А-1)* = (А*)-1.
- Рассмотрим в пространстве V2 линейный оператор Rφ поворота вектора на угол φ, 0 < φ < π. Найдите оператор, сопряженный к оператору Rφ.
- Пусть Ε - евклидово пространство, е - произвольный, вообще говоря, неортогональный базис в Ε, Г - матрица Грама для системы векторов е. Докажите, что если линейный оператор А в базисе е имеет матрицу А, то сопряженный к нему оператор А* имеет в том же базисе матрицу А* = Г-1ATГ.
- В базисе
- Докажите, что для любого евклидова пространства Ε отображение L(Ε,Ε) → L(Ε,Ε), сопоставляющее линейному оператору из L(Ε,Ε) ему сопряженный, является изоморфизмом линейного пространства L(Ε,Ε). Зависит ли этот изоморфизм от выбора базиса в евклидовом пространстве Ε? Когда этот изоморфизм является тождественным отображением?
- Для симметрической матрицы
b1 = (1, 1, 1, 1), b2 = (1, 1, 1,0),
b3 = (1, 1, 0, 0), b4 = (1, 0, 0, 0)
линейного арифметического пространства Rn матрица линейного оператора А имеет вид
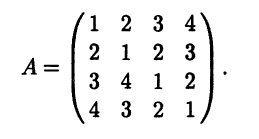
Найдите матрицу сопряженного оператора А* в том же базисе (b1 b2 b3 b4). В пространстве Rn предполагается стандартное скалярное произведение.
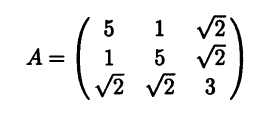
найдите подобную ей диагональную матрицу А' = Р-1АР и соответствующую матрицу Р.
Линейные операции над векторами
Базис. Cкалярное произведение
Векторное и смешанное произведения векторов
Декартова система координат. прямая на плоскости
Плоскость в пространстве
Прямая в пространстве
Кривые второго порядка — I
Кривые второго порядка — II
Поверхности второго порядка
Матрицы и операции с ними
Обратная матрица
Ранг матрицы
Системы линейных алгебраических уравнений
Свойства решений однородных и неоднородных СЛАУ