Свойства собственных векторов
Теория- Автор
- Издательство
Теорема 5.5. Пусть собственные значения λ1, ..., λr линейного оператора А попарно различны. Тогда система соответствующих им собственных векторов е1, ... , еr линейно независима.
◄ Доказательство опирается на метод математической индукции, проводимый по количеству r векторов в системе. При r = 1 утверждение теоремы верно, так как линейная независимость системы из одного вектора означает, что этот вектор ненуле-вой, а собственный вектор, согласно определению 5.3, является ненулевым.
Пусть утверждение верно при r = m, т.е. для произвольной системы из т собственных векторов e1, ..., еm. Добавим к системе векторов еще один собственный вектор em+1, отвечающий собственному значению λm+1, и докажем, что расширенная таким способом система векторов останется линейно независимой. Рассмотрим произвольную линейную комбинацию полученной системы собственных векторов и предположим, что она равна нулевому вектору:
α1е1 + ... + αmеm + αm+1em+1 = 0. (5.7)
К равенству (5.7) применим линейный оператор А и в результате получим еще одно векторное равенство
α1Ае1 +... + αmАеm + αm+1Aem+1 = 0.
Учтем, что векторы e1, ..., em+1 являются собственными:
α1λ1e1 + ... + αmλmem + αm+1λm+1em+1 = 0. (5.8)
Умножив равенство (5.7) на коэффициент λm+1 и вычтя его из равенства (5.8), получим линейную комбинацию векторов е1, ..., em, равную нулевому вектору:
α1(λ1 - λm+1)e1 + ... + αm(λm - λm+1)em = 0.
Вспоминая, что система векторов e1, ..., em, по предположению, линейно независима, делаем вывод, что у полученной линейной комбинации все коэффициенты равны нулю:
αk (λk - λm+1) = 0, k = 1,m. (5.9)
Поскольку все собственные значения λi попарно различны, то из равенств (5.9) следует, что α1 = α2 = ... = αm = 0. Значит соотношение (5.7) можно записать в виде αm+1em+1 = 0, а так как вектор em+1 ненулевой (как собственный вектор), то αm+1 = 0. В итоге получаем, что равенство (5.7) выполняется лишь в случае, когда все коэффициенты ai, i = 1, m+1, равны нулю. Тем самым мы доказали, что система векторов e1, ..., em, em+1 линейно независима. ►
Теорема 5.6. Матрица линейного оператора А, действующего в линейном пространстве, в данном базисе является диагональной тогда и только тогда, когда все векторы этого базиса являются собственными для оператора А.
◄ Пусть А - матрица линейного оператора А в базисе b = (b1 ... bn). Согласно определению 4.4, j-м столбцом матрицы А является столбец координат вектора Abj.
Если матрица А является диагональной, то произвольно взятый ее j-и столбец имеет вид (0 ... 0 μj 0 ... 0)T (единственный ненулевой элемент может стоять на j-м месте). Для вектора Abj получаем представление
Abj = b(0 ... 0 μj 0 ... 0)T = μjbj,
которое как раз и означает, что вектор bj является собственным с собственным значением μj. Значит, все базисные векторы являются собственными, а все диагональные элементы матрицы А являются собственными значениями.
Верно и обратное. Если каждый вектор bj является собственным для линейного оператора А и ему отвечает собственное значение λj, то
Abj = λjbj = b(0 ... 0 λj 0 ... 0)T,
т.е. в матрице оператора А в этом базисе равны нулю все элементы, кроме диагональных, а диагональный элемент в j-м столбце равен λj. ►
Следствие 5.1. Если характеристическое уравнение линейного оператора, действующего в n-мерном линейном пространстве, имеет n попарно различных действительных корней, то существует базис, в котором матрица этого оператора является диагональной.
◄ Каждый действительный корень характеристического урав-нения является собственным значением линейного оператора.
Каждому из таких корней можно сопоставить хотя бы по одно-му собственному вектору. Система выбранных таким образом векторов, согласно теореме 5.5, является линейно независимой, а так как количество n векторов в ней равно размерности линейного пространства, она является базисом. Этот базис состоит из собственных векторов. Согласно теореме 5.6, матрица линейного оператора в этом базисе имеет диагональный вид. ►
Следствие 5.2. Если характеристическое уравнение квадратной матрицы порядка n имеет n попарно различных действительных корней, то эта матрица подобна некоторой диагональной.
◄ Пусть матрица А порядка n имеет n различных действительных корней. Выберем произвольное n-мерное линейное пространство L, зафиксируем в нем некоторый базис b = (b1 ... bn) и рассмотрим линейный оператор А, матрицей которого в базисе b является матрица А. По теореме 5.6 существует базис, в котором матрица A' этого оператора диагональна. Согласно теореме 4.6, матрицы А и А' подобны. Отметим, что на диагонали матрицы А' стоят все попарно различные собственные значения матрицы А. ►
Если характеристическое уравнение линейного оператора имеет кратные действительные корни, то такой линейный оператор может иметь диагональную матрицу в некотором базисе, но так бывает не всегда.
Пример 5.7. В двумерном линейном пространстве (например, в R2) рассмотрим линейные операторы, матрицы которых в некотором базисе имеют вид
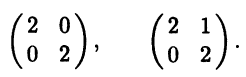
Характеристические уравнения этих операторов совпадают и имеют вид (λ - 2)2 = 0. Поэтому оба оператора имеют единственное собственное значение λ = 2 кратности 2. Матрица первого линейного оператора уже имеет диагональный вид, т.е. исходный базис состоит из собственных векторов этого оператора. Можно показать, что любой ненулевой вектор для этого оператора является собственным и потому для него любой базис есть базис из собственных векторов. У второго линейного оператора все собственные векторы отвечают собственному значению 2, но собственное подпространство линейного оператора для этого собственного значения одномерно. Следовательно, найти два линейно независимых собственных вектора для этого линейного оператора невозможно и базиса из собственных векторов не существует. #
При изучении заданного линейного оператора появляется мысль выбрать такой базис, в котором его матрица выглядит наиболее просто. Из вышеизложенного следует, что в определенных ситуациях линейный оператор в некотором базисе имеет диагональную матрицу. Чтобы это было так, оператор должен иметь базис из собственных векторов. Изменение бази-са вызывают замену матрицы оператора подобной ей. Замену матрицы А диагональной матрицей А', подобной А, называют приведением матрицы А к диагональному виду.
Задача приведения матрицы к диагональному виду может рассматриваться самостоятельно, вне зависимости от изучения конкретного линейного оператора. Она состоит в подборе для данной матрицы А такой невырожденной матрицы Р, что матрица А' = Р-1АР является диагональной.
Пример 5.8. Выясним, можно ли привести к диагональному виду матрицу
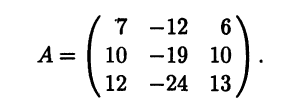
Если это возможно, найдем соответствующую диагональную матрицу и матрицу Р преобразования подобия.
Найдем собственные значения данной матрицы. Ее характеристическое уравнение имеет вид
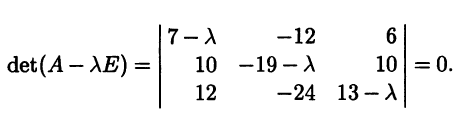
Раскрывая определитель и решая характеристическое уравнение, находим его корни: λ1 = -1, λ2 = λ3 = 1. Видим, что имеются два собственных значения, причем одно из них кратности 2.
Матрицу можно привести к диагональному виду, если сумма размерностей всех собственных подпространств (в данном случае матрицы, см. замечание 5.1) равна размерности линейного пространства, в нашем случае - трем. Отметим без доказательства, что размерность собственного подпространства линейного оператора (матрицы) не превышает кратности соответствующего собственного значения. Проверим это на собственном подпространстве, отвечающем собственному значению λ1, для чего вычислим ранг матрицы А - λ1Е:
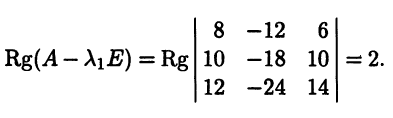
Значит, размерность первого собственного подпространства равна 3 - 2 = 1.
Аналогично находим размерность второго собственного подпространства. Вычисляем ранг соответствующей матрицы А - λ2Е:
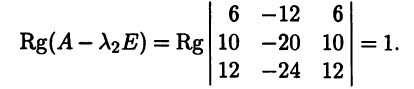
Размерность второго собственного подпространства равна 3 - 1 = 2.
Сумма размерностей обоих подпространств равна трем. Следовательно, базис из собственных векторов существует. Он собирается из базисов собственных подпространств. Чтобы его построить, нужно для каждого собственного значения А найти фундаментальную систему решений СЛАУ (А - λЕ)х = 0. Фундаментальная система решений представляет собой базис линейного пространства решений однородной СЛАУ, в нашем случае собственного подпространства матрицы.
Для собственного значения λ1 = - 1 получаем систему
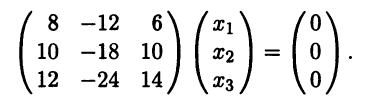
Ранг матрицы системы равен двум, поэтому фундаментальная система состоит из одного столбца. Например, можно взять столбец (3 5 6)T.
Для собственного значения λ2 = 1 получаем систему
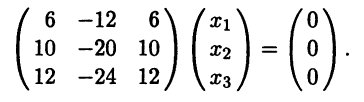
Ранг матрицы системы равен единице, поэтому фундаментальная система состоит из двух столбцов. Например, фундаментальную систему решений составляют столбцы (2 1 0)T и (0 1 2)T.
Таким образом, базисом из собственных векторов матрицы А является система
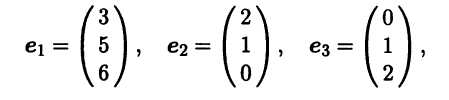
а сама матрица А подобна диагональной матрице
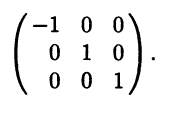
Отметим, что матрица Р преобразования подобия представляет собой матрицу перехода из одного базиса в другой, т.е. ее столбцы представляют собой столбцы координат векторов нового базиса, записанные в старом. В нашем случае столбцы матрицы Р определяются векторами "нового" базиса e1, e2, е3:
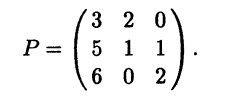
Пример 5.9. Линейный оператор, действующий в трехмерном линейном пространстве, в некотором базисе имеет матрицу
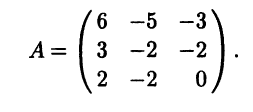
Можно ли, изменив базис, привести матрицу этого оператора к диагональному виду?
Составляем характеристическое уравнение линейного оператора:
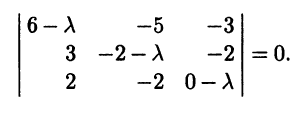
Раскрывая определитель, получаем
λ3 - 4λ2 + 5λ - 2 = 0.
Корнями характеристического уравнения являются числа λ1 = 1 кратности 2 и λ2 = 2. Для определения размерностей собственных подпространств линейного оператора, отвечающих этим двум значениям, вычислим ранги соответствующих матриц:
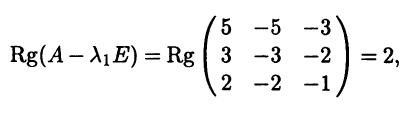
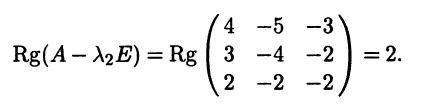
Оба собственных подпространства линейного оператора, отвечающие двум собственным значениям, имеют размерность 3 - 2 = 1. Поэтому линейно независимая система из собственных векторов данного оператора может содержать максимум два вектора и по соображениям размерности не может быть базисом.
Дополнение 5.1. Жорданова нормальная форма
При исследовании линейного оператора, действующего в линейном пространстве, желательно выбирать базис так, чтобы матрица линейного оператора имела наиболее простой вид. Если линейный оператор имеет базис из собственных векторов, то его матрица в некотором базисе является диагональной (теорема 5.6). В частности, это верно в случае, когда все корни характеристического уравнения линейного оператора действительные и различные (см. следствие 5.1).
Матрица диагонального вида - наиболее простая, но не всякий линейный оператор может иметь такую матрицу (см. пример 5.7). Линейный оператор, который не может быть приведен к диагональному виду (т.е. его матрица ни в одном базисе не является диагональной), имеет характеристическое уравнение, у которого есть комплексные или кратные действительные корни.
Приведение матрицы линейного оператора к простому виду связано со структурой его инвариантных подпространств.
Теорема 5.7. Пусть Н1 и H2 - инвариантные подпространства линейного оператора А: L → L, причем Н1 ⊕ Н2 = L. Тогда в некотором базисе b матрица А этого оператора А имеет блочно-диагональный вид:
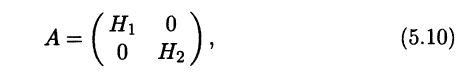
где 0 обозначает нулевые блоки соответствующего типа, а квадратные блоки H1, Н2 имеют порядки dimH1 и dimН2 соответственно.
◄ Выберем в линейных подпространствах H1 и Н2 базисы f = (f1 ... fl) и g = (g1 ... gk). В совокупности эти два базиса дают базис b всего пространства L (см. доказательство теоремы 2.5). Так как H1 - инвариантное подпространство линейного оператора А, вектор Аfi, i = 1,l, попадает в H1 и поэтому является линейной комбинацией системы векторов f. Другими словами, координаты вектора Afi в базисе b, соответствующие векторам равны нулю. Аналогично координаты векторов Agj, j = 1,k, в базисе b, соответствующие векторам fi, также равны нулю. Значит, в базисе b матрица А оператора А имеет вид (5.10). ►
Следствие 5.3. Если H1, ... , Нs - инвариантные подпространства линейного оператора А: L → L, причем Н1 ⊕ ... ⊕ Hs = L, то в некотором базисе матрица оператора А имеет блочно-диагональный вид
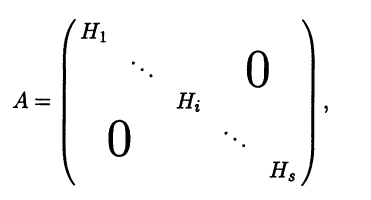
где квадратный блок Hi имеет порядок dimHi, i = 1,s, а остальные блоки являются нулевыми.
◄ Выберем в каждом из инвариантных подпространств Hi базис. Все базисы в совокупности образуют базис пространства L, в котором оператор А будет иметь матрицу указанного вида. ►
Остановимся на случае, когда характеристическое уравне-ние линейного оператора имеет лишь простые корни, среди которых, вообще говоря, есть и комплексные. Так как характеристическое уравнение линейного оператора имеет действительные коэффициенты, каждому комплексному корню α + iβ этого уравнения соответствует комплексно сопряженный корень α - iβ той же кратности [I].
Теорема 5.8. Любой паре комплексно сопряженных корней характеристического уравнения линейного оператора соответствует двумерное инвариантное подпространство этого оператора.
◄ Зафиксируем в линейном пространстве L некоторый базис b и рассмотрим матрицу А линейного оператора А в этом базисе. Пусть λ = α + iβ, β ≠ 0, - комплексный корень характеристического уравнения линейного оператора А. Тогда det(A - λЕ) = 0 и система линейных алгебраических уравнений (СЛАУ) (А - λЕ)х = 0 с комплексными коэффициентами имеет ненулевое решение x, которое можно записать в виде х = u + iϑ, разделив действительные и мнимые части у элементов столбца х.
Столбец ϑ не является нулевым, так как в противном случае х = u, и Аu = λu. Мы видим, что действительные элементы столбца Аu получаются из действительных элементов столбца и умножением на комплексное число λ, а это возможно лишь в случае, когда u = 0. Но это заключение противоречит выбору столбца х.
Столбцы u и ϑ линейно независимы. Действительно, если они линейно зависимы, то μu + vϑ = 0, где одно из чисел μ и v отлично от нуля. Мы можем утверждать, что μ ≠ 0, так как в противном случае vϑ =0. Но ϑ ≠ 0, значит v = 0. Получилось, что оба коэффициента μ и v являются нулевыми.
Итак, μ ≠ 0, и поэтому u = kϑ, где к = - v/μ ∈ R. Следовательно, x = u + iϑ = (k + i)ϑ. Так как Ах = λх, то А((k + i)ϑ) = λ(k + i)ϑ, и мы, сокращая равенство на k + i, находим, что Aϑ = λϑ. Как мы уже знаем, для комплексного λ такое равенство невозможно.
В равенстве Ах = λх сделаем замены λ = α + iβ, х = u + iϑ: А(u + iϑ) = (α + iβ) (u + iϑ). Разделив действительные и мнимые части, получим два матричных уравнения
Аu = αu - βϑ, Aϑ = βu + αϑ. (5.11)
Рассмотрим векторы u и ϑ, которые в базисе b имеют столбцы координат u и ϑ. Эти векторы образуют линейно независимую систему, так как линейно независимы столбцы u и ϑ. Кроме того, Аu = αu - βϑ, Aϑ = βu + αϑ, так как в матричной записи это совпадает с (5.11). Полученные соотношения означают, что двумерное линейное подпространство Н = span{u, ϑ} является инвариантным подпространством линейного оператора А. ►
Для любых действительных α и β обозначим
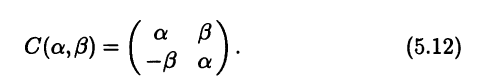
Теорема 5.9. Если характеристическое уравнение линей-ного оператора А: L → L имеет р различных пар комплексно сопряженных корней αj ± iβj, j = 1,p, и q различных действительных корней μj, j = 1,q, 2p + q = n = dimL, то в некотором базисе матрица А этого оператора А имеет вид
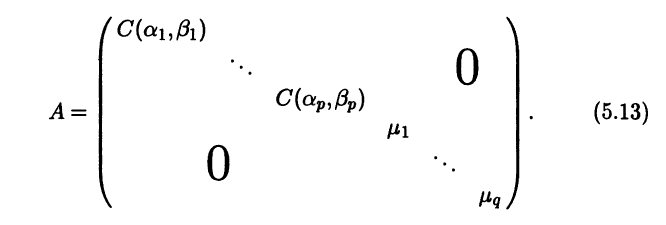
◄ Каждой паре комплексно сопряженных корней αj ± iβj характеристического уравнения соответствует двумерное инвариантное подпространство Pj оператора А с базисом uj, ϑj (см. доказательство теоремы 5.8). Каждому собственному значению μj соответствует одномерное собственное подпространство Qj линейного оператора А. Можно показать, что все эти подпространства образуют прямую сумму, так как пе-ресечение любой пары таких подпространств содержит лишь нулевой вектор. Учитывая, что сумма размерностей этих подпространств равна 2р + q = n = dimL, заключаем, что
P1⊕ ... ⊕ Pp ⊕ Q1 ⊕ ... ⊕ Qq = L.
Согласно следствию 5.3, в некотором базисе матрица А оператора А имеет блочно-диагональный вид, причем каждый диагональный блок представляет собой матрицу ограничения оператора А на соответствующее инвариантное подпространство. В случае двумерного подпространства Pj в базисе uj, ϑj эта матрица равна C(αj,βj) (см. (5.12)), а в случае одномерного инвариантного пространства Qj такой блок есть просто число, представляющее собой собственное значение μj. ►
Следствие 5.4. Если характеристическое уравнение квадратной матрицы А порядка n имеет р различных пар комплексно сопряженных корней αj ± iβj, j = 1,p, р, и q различных действительных корней μj, j = 1,q, 2p + q = n, то эта матрица подобна некоторой блочно-диагональной матрице вида (5.13).
◄ Указанная матрица А является матрицей некоторого линейного оператора А, характеристическое уравнение которого имеет различные корни. Согласно теореме 5.9, в некотором базисе оператор А имеет матрицу А' блочно-диагонального вида (5.13) . Матрицы А' и А подобны как матрицы одного оператора. ►
Если характеристическое уравнение оператора имеет кратные корни, действительные или комплексные, то инвариантные подпространства такого оператора имеют более сложную структуру. Рассмотрим два типа специальных матриц.
Для произвольного действительного числа μ введем обозначение матрицы порядка s:
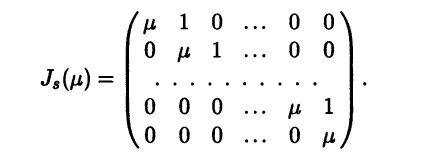
У этой матрицы все диагональные элменты равны ц, над главной диагональю расположены элементы 1, а все остальные равны нулю. В случае s = 1 рассматриваемая матрица сводится к единственному числу μ.
Для любого комплексного числа λ = α + iβ (β ≠ 0) введем обозначение блочной матрицы порядка 2r:
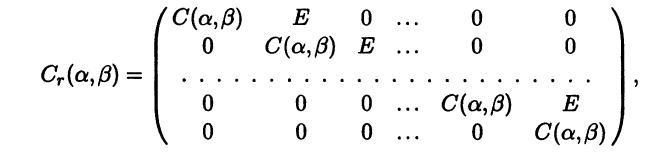
где C1(α,β) = С(α,β) - квадратная матрица порядка 2 вида (5.12). Все остальные блоки также являются квадратными матрицами порядка 2, Е обозначает единичную матрицу, а 0 - нулевую.
Блочно-диагональную матрицу вида
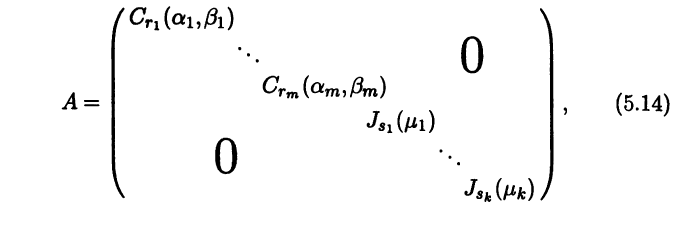
где αj, βj (j = 1,m) и μl (l = 1,k) - действительные числа, называют жордановой, ее диагональные блоки - жордановыми клетками. Жорданову матрицу А', подобную данной матрице А, называют жордановой нормальной формой (жордановой канонической формой) матрицы А.
Жорданова нормальная форма определяется неоднозначно, так как подходящими преобразованиями подобия можно пере-ставлять диагональные блоки (перестановка блоков в матрице линейного оператора вызывается перёстановкой соответствую-щих векторов базиса). Среди жордановых клеток жордановой матрицы могут встречаться одинаковые. Однако можно утвер-ждать, что если две жордановы матрицы подобны, то одна получается из другой перестановкой диагональных блоков. Это объясняется тем, что каждая жорданова клетка вида Jj(μj) определяется собственным значением μj матрицы, а жорданова клетка Cj (αj, βj) - комплексным корнем λj = αj + iβj характеристического уравнения матрицы. Частным случаем жорда-новой матрицы является матрица вида (5.13) (когда все корни характеристического уравнения простые) и диагональная матрица (все корни действительные, а все жордановы клетки имеют порядок 1).
Теорема 5.10. Каждая матрица имеет жорданову нормальную форму.
Вопросы и задачи
- Найдите собственные векторы и собственные значения линейного оператора, имеющего в некотором базисе матрицу:
- В примерах в), д)-к) постройте базис из собственных векторов и запишите матрицу линейного оператора в этом базисе.
- Выясните, приводится ли к диагональному виду данная матрица:
- Пусть линейный оператор, действующий в n-мерном линейном пространстве, имеет в некотором базисе матрицу А. Пусть λ1, λ2, ..., λn - собственные значения этого оператора. Найдите собственные значения и собственные векторы линейного оператора, матрицей которого в том же базисе является: а) A2; б) А-1
- В линейном пространстве квадратных матриц порядка 2 содержится линейная оболочка матриц Аk, k = 0,100. Найдите размерность этой линейной оболочки для матрицы
- Докажите, что для каждого собственного значения А линейного оператора λ имеет место равенство £(А, А) = ker(A - λI).
- Докажите, что кратность собственного значения Л линейного оператора А не меньше размерности соответствующего собственного подпространства £(А, λ) этого оператора.
- Докажите теорему Кэли - Гамильтона в случае квадратной матрицы, все корни характеристического уравнения которой действительны и попарно различны.
- Сформулируйте теорему Кэли - Гамильтона для линейных операторов и доказать ее в случае линейного оператора, имеющего базис из собственных векторов.
- Докажите, что поворот вектора на плоскости на угол 2φ можно реализовать за три последовательно выполняемых шага: поворот вектора на угол φ; растяжение с коэффициентом 2 cosφ; прибавление вектора, противоположного исходному.
- Докажите, что любой линейный оператор в пространстве V3 имеет собственный вектор.
- Приведите пример линейного оператора, не имеющего собственных векторов. Какой может быть размерность линейного пространства, в котором есть такие операторы?
- Докажите, что для любого ненулевого вектора с ∈ V3 линейный оператор А: V3 → V3, определяемый соотношением Ах = x × с, имеет единственное собственное значение, равное нулю.
- Пусть Н - линейное подпространство евклидова пространства Ε. Рассмотрим линейный оператор ортогонального проектирования Рх = х°, где х = х° + x⊥, х° ∈ H, х⊥ ∈ Н⊥, - разложение произвольного вектора х на его ортогональную проекцию х° и ортогональную составляющую x⊥. Найдите собственные значения и собственные векторы этого линейного оператора.
- Докажите, что нуль является собственным значением любой кососимметрической матрицы нечетного порядка.
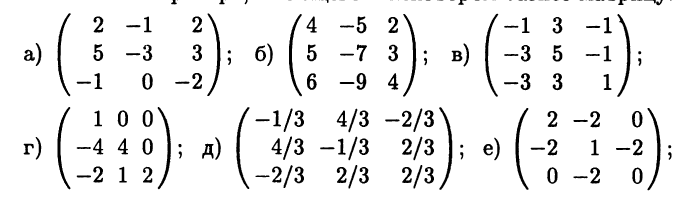
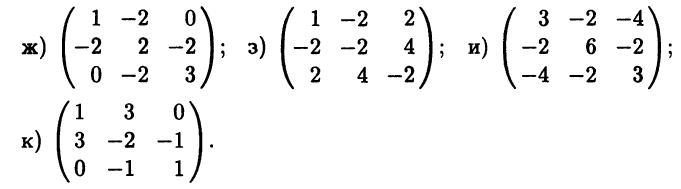
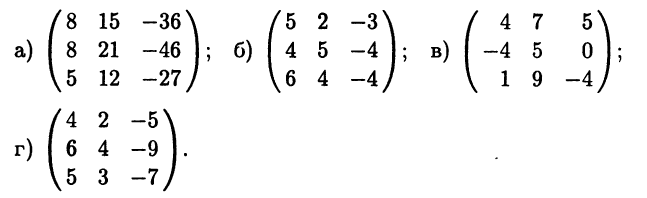
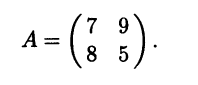
Линейные операции над векторами
Базис. Cкалярное произведение
Векторное и смешанное произведения векторов
Декартова система координат. прямая на плоскости
Плоскость в пространстве
Прямая в пространстве
Кривые второго порядка — I
Кривые второго порядка — II
Поверхности второго порядка
Матрицы и операции с ними
Обратная матрица
Ранг матрицы
Системы линейных алгебраических уравнений
Свойства решений однородных и неоднородных СЛАУ