Вычисление собственных значений и собственных векторов

Характеристическое уравнение линейного оператора А: L → L, действующего в n-мерном линейном пространстве L, - это алгебраическое уравнение n-й степени с действительными коэффициентами. Среди его корней могут быть комплексные числа, но эти корни не относят к собственным значениям линейного оператора, так как, согласно определению, собственное значение линейного оператора - действительное число. Чтобы комплексные корни характеристического уравнения можно было рассматривать как собственные значения линейного оператора, в линейном пространстве должно быть определено умножение вектора на любые комплексные числа.

Как следует из доказательства теоремы 5.3, чтобы вычислить собственные значения линейного оператора А и найти его собственные векторы, нужно выполнить следующие операции:

- выбрать в линейном пространстве базис и сопоставить А матрицу А этого линейного оператора в выбранном базисе;

- составить характеристическое уравнение det (А - λЕ) = 0 и найти все его действительные корни λ_k, которые и будут собственными значениями линейного оператора;

- для каждого собственного значения λ_k найти фундаментальную систему решений для однородной системы линейных алгебраических уравнений (СЛАУ) (А - λ_kЕ)х = 0. Столбцы фундаментальной системы решений представляют собой координаты векторов некоторого базиса в собственном подпространстве £(А, λ_k) линейного оператора А.

Любой собственный вектор с собственным значением λ_k принадлежит подпространству £(А,λ_k), и, следовательно, найденный базис в этом подпространстве позволяет представить любой собственный вектор с собственным значением λ_k.

Пример 5.4. Найдем собственные векторы и собственные значения линейного оператора А, имеющего в некотором базисе матрицу

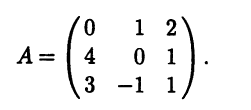
В соответствии с описанной процедурой необходимо выполнить три действия. Первое действие можно опустить, так как оператор уже представлен своей матрицей в некотором базисе. Выполняем дальнейшие действия.

2) Находим собственные значения, решая характеристическое уравнение матрицы:

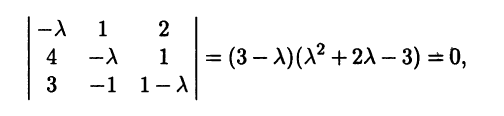
откуда λ₁ = -3, λ₂ = 1, λ₃ = 3.

3) Находим столбцы координат собственных векторов, ре-шая для каждого из трех собственных значений однородную СЛАУ

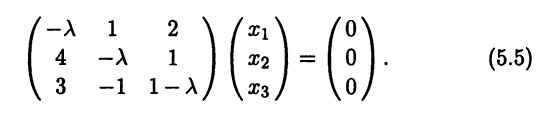
3а) Для λ = λ₁ = -3 система (5.5) имеет вид

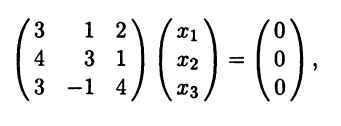
или

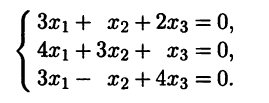
Ранг матрицы этой системы равен 2:

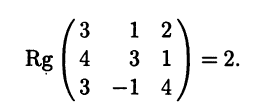
Поэтому размерность линейного пространства решений систе-мы равна 3 - 2 = 1. Фундаментальная система решений содер-жит одно решение, например

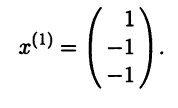
Все множество собственных векторов линейного оператора с собственным значением λ₁ = -3 в координатной форме имеет вид

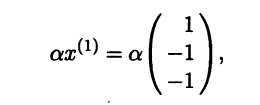
где α - произвольное ненулевое действительное число.

3б) При λ = λ₂ = 1 система (5.5) имеет вид

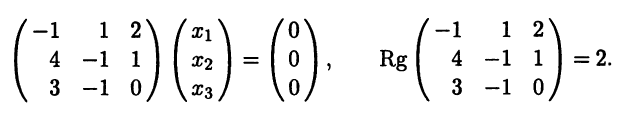
Как и в предыдущем случае, размерность линейного простран-ства решений равна 2 - 1 = 1 и фундаментальная система решений содержит одно решение. Выберем следующее:

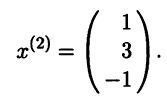
Все множество собственных векторов с собственным значением λ = -1 в координатной форме имеет вид

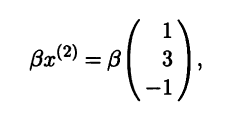
где β - произвольное ненулевое действительное число.

3в) Для λ = λ₃ = 3 аналогично предыдущим двум случаям находим столбец координат одного из собственных векторов, например

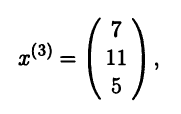
который порождает собственное подпространство линейного оператора А, отвечающее собственному значению λ = 3.

Пример 5.5. Найдем собственные значения линейного оператора А, действующего в n-мерном линейном пространстве, матрица А которого в некотором базисе является верхней треугольной порядка n:

причем все ее диагональные элементы а_ii попарно различны, т.е. а_ii ≠ a_jj при i ≠ j.

Составляем характеристическое уравнение матрицы А:

det(А - λЕ) = (а₁₁ - λ)(а₂₂ - λ) ... (а_nn - λ) = 0

(определитель верхней треугольной матрицы равен произведе-нию ее диагональных элементов). Находим все действительные корни этого уравнения:

λ_k = a_kk, k = 1,n

Как видим, линейный оператор А имеет n попарно различных собственных значений.

Отметим, что пересечение любых двух собственных подпространств линейного оператора содержит лишь нулевой вектор, так как собственный вектор не может отвечать двум различным собственным значениям. Поэтому собственные подпространства линейного оператора образуют прямую сумму, а размерность прямой суммы линейных подпространств, согласно следствию из теоремы 2.5, равна сумме их размерностей. Из этих соображений следует, что каждое из n собственных подпространств рассматриваемого линейного оператора является одномерным, так как их размерность не может быть меньше, но если бы одно из подпространств имело размерность больше единицы, то суммарная их размерность превышала бы размерность самого линейного пространства.

Итак, все собственные подпространства линейного операто-ра в нашем случае одномерны. Рассмотрим то из них, которое отвечает собственному значению λ_r = а_rr, где 1 ≤ r ≤ n. Соответствующий собственный вектор имеет столбец координат, который является ненулевым решением однородной СЛАУ

(А - a_rrЕ)х = 0. (5.6)

Достаточно очевидно, что ранг матрицы системы (5.6) равен n - 1, а базисный минор для этой матрицы получается вычер-киванием r-й строки и r-го столбца.

Наиболее просто решение системы (5.6) выглядит для r = 1. В этом случае собственным является вектор x₁ со столбцом координат (1 0 ... 0)^T . При r = 2 все координаты собственного вектора, начиная с третьей, будут равны нулю, так как они удовлетворяют системе

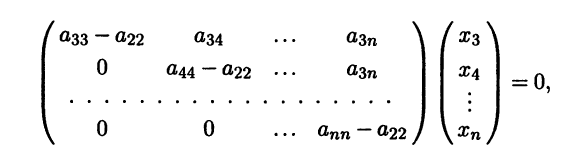
получающейся выбрасыванием первых двух уравнений. Второе уравнение вытекает из всех последующих и может быть опуще-но, а первое уравнение определяет связь между первыми двумя координатами. Мы получаем, что собственному значению а₂₂ отвечает вектор x₂ со столбцом координат (-a₁₂ a₁₁ 0 ... 0)^T . Собственному значению a₃₃ отвечает вектор x₃ со столбцом координат (x₁₃ x₂₃ x₃₃ 0 ... 0)^T , у которого лишь первые три координаты отличны от нуля. Эти три координаты удовлетворяют однородной системе из двух уравнений

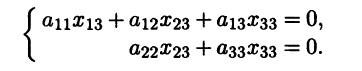
Эти рассуждения можно продолжить.

Пример 5.6. Преобразование поворота в V₃ на заданный острый угол вокруг некоторой оси - это линейный оператор. Его собственными векторами являются векторы, коллинеарные оси поворота. Например, если поворот выполняется вокруг оси Оz, то матрица оператора в базисе i, j, k будет иметь вид

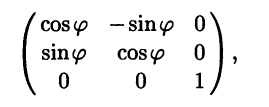
а его собственными векторами будут векторы со столбцами координат вида λ(0 0 1)^T , λ ≠ 0.

1. Линейные операции над векторами

2. Базис. Cкалярное произведение

3. Векторное и смешанное произведения векторов

4. Декартова система координат. прямая на плоскости

5. Плоскость в пространстве

6. Прямая в пространстве

7. Кривые второго порядка — I

8. Кривые второго порядка — II

9. Поверхности второго порядка

10. Матрицы и операции с ними

11. Обратная матрица

12. Ранг матрицы

13. Системы линейных алгебраических уравнений

14. Свойства решений однородных и неоднородных СЛАУ