Матрица линейного оператора

Пример 4.3 более глубок, чем это может показаться с первого взгляда. Фактически любой линейный оператор можно интерпретировать как линейный оператор, описанный в этом примере, т.е. действие линейного оператора сводится к умножению столбца координат вектора на матрицу. Поясним это подробнее.

Пусть задан линейный оператор А: L → L, т.е. линейное преобразование n-мерного линейного пространства L в себя. Выберем базис b = (b₁ ... b_n) в L. Действие линейного оператора полностью определено, если известны образы векторов базиса. Действительно, если вектор х имеет координаты х = (x₁ ... х_n)^T , то

Ах = A(x₁b₁ + ... + х_nb_n) = x₁(Ab₁) +... + х_n(Аb_n),

т.е., зная векторы Ab_i, мы можем найти образ любого вектора x линейного пространства L.

Рассмотрим действие линейного оператора А на векторы базиса b. Обозначим столбцы координат векторов Ab_ix в базисе через а_i, a_i = (а_1i ... а_in) , i = 1,n. Тогда

Ab_i = ba_i, i = 1,n.

Определение 4.4. Матрицу А = (а₁ ... a_n), составленную из координатных столбцов векторов Ab₁, ... , Ab_n в базисе b = (b₁ ... b_n) называют матрицей линейного оператора А в базисе b.

Матрица линейного оператора А: L → L является квадратной, ее порядок совпадает с размерностью линейного пространства L.

Рассмотрим несколько примеров линейных операторов и их матриц.

Пример 4.7. Матрицей нулевого оператора Θ: L → L независимо от выбора базиса является нулевая матрица соответствующего типа. Действительно, образом любого вектора в случае нулевого оператора является нулевой вектор. Поэтому матрица нулевого оператора в любом базисе должна состоять из нулевых столбцов.

Пример 4.8. Матрица тождественного оператора I также не зависит от выбора базиса и в любом базисе является единичной. Действительно, взяв произвольный базис b = (b₁ ... b_n), заключаем, что при i = 1,n

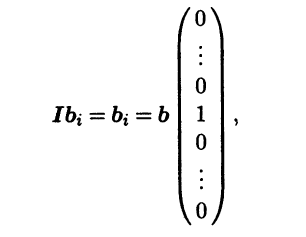
где единица в последнем столбце стоит на i-м месте. Видно, что столбец координат вектора Ib_i является i-м столбцом единичной матрицы.

Теорема 4.3. Пусть А: L → L - линейный оператор. Тогда столбец у координат вектора у = Ах в данном базисе b линейного пространства L равен произведению Ах матрицы А оператора А в базисе b на столбец х координат вектора x в том же базисе: у = Ах.

◄ Выберем произвольный вектор х = х₁b₁ + ... + х_nb_n. Его образом будет вектор

у = Ах = A(x₁b₁ + ... + x_nb_n) = x₁(Ab₁) + ... + х_n(Аb_n) = x₁(a₁₁b₁ + ... + a_n1b_n) + ... + x_n(a_1nb₁ + ... + a_nnb_n) = (а₁₁x₁ + ... + a_1nx_n)b₁ + ... + (a_n1x₁ + ... + a_nnx_n)b_n.

Столбец координат вектора Ax в базисе b имеет вид

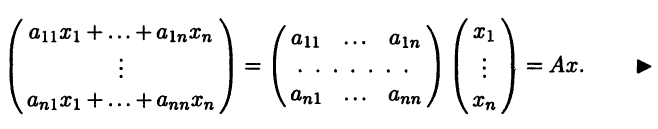
Запись у = Ах из формулировки теоремы 4.3 удобно называть матричной формой записи действия линейного оператора А в базисе b.

Замечание 4.1. Выкладки, приведенные в доказательстве теоремы, можно упростить, если использовать матричные обо-значения и правила выполнения матричных операций. Полагая, что строка образов базисных векторов (Ab₁ ... Ab_n) получается "умножением" строки векторов b слева на оператор А:

(Аb₁ ... Аb_n) = Аb,

получаем

Ab = (Ab₁ ... Ab_n) = (ba₁ ... ba_n) = b(a₁ ... а_n) = bА,

так как ba_i - матричная запись разложения вектора Ab_i по базису b, i = 1,n. Здесь мы использовали технику операций с блочными матрицами.

Взяв произвольный вектор х = bх, получаем

Ах = А(bх) = (Аb)х = (bА)х = b(Ах).

Это означает, что столбец Ах является столбцом координат вектора Ах.

Пример 4.9. Рассмотрим отображение А: V₃ → V₃, которое каждый вектор х преобразует в его векторное произведение Ах = х × i на орт i оси Ох. В силу свойств векторного произведения это отображение - линейный оператор. Найдем матрицу А этого линейного оператора в (правом) ортонорми- рованном базисе i, j, k. Для этого надо найти образы базисных векторов и разложить их по тому же базису. Поскольку Ai = i × i = 0, то первый столбец в матрице А нулевой. Далее получаем второй столбец матрицы А:

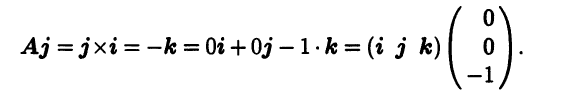
Затем третий столбец:

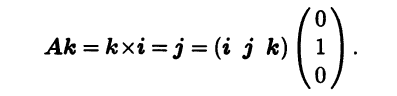
Итак, матрица А имеет вид

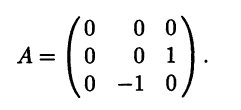
Действие линейного оператора А на вектор х можно теперь записать как умножение столбца координат (х у z)^T вектора х слева на матрицу оператора:

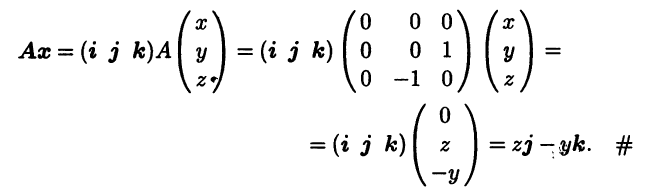
Матрица линейного оператора полностью характеризует линейный оператор. В то же время, какую бы квадратную матрицу порядка n мы ни взяли, она будет матрицей некоторого линейного оператора в заданном базисе n-мерного линейного пространства (см. пример 4.3). Таким образом, между линейными операторами, действующими в данном n-мерном линейном пространстве L и квадратными матрицами порядка n существует соответствие, которое является взаимно однозначным, что и утверждает следующая теорема.

Теорема 4.4. Пусть b - произвольный базис в n-мерном линейном пространстве L. Различным линейным операторам А и В, действующим в пространстве L, соответствуют и различные матрицы в базисе b. Любая квадратная матрица А порядка n является матрицей некоторого линейного оператора, действующего в линейном пространстве L.

◄ Если матрицы А и В операторов А и В в базисе b совпадают, то, согласно теореме 4.3, для любого вектора х со столбцом координат х

Ах = bАх = bВх = Вх,

т.е. образы произвольного вектора при двух отображениях совпадают. Следовательно, совпадают и сами отображения.

Пусть А = (a_ij) - произвольная квадратная матрица порядка n. Определим отображение А: L → L согласно формуле А(х) = bАх, где х - столбец координат вектора х. Несложно проверить, что заданное таким образом отображение является линейным оператором. Действительно, для любых векторов х,у ∈ L и любых действительных чисел λ, μ

А(λx + μу) = bА(λх + μу) = λ(bАx) + μ(bАу) = λА(х) + μА(у).

В этой выкладке мы использовали теорему 1.3 и свойства умножения матриц. Вычислив для i = 1,n столбец координат образа i-го вектора из базиса b

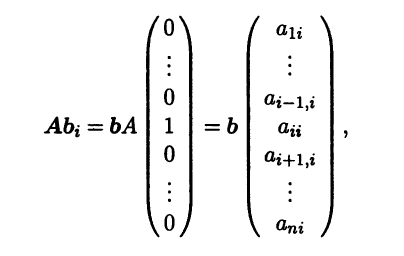
где единица стоит в i-й строке, убеждаемся, что он совпадает с i-м столбцом матрицы А и поэтому матрица заданного линейного оператора совпадает с исходной матрицей А. ►

Теорема 4.5. Ранг матрицы линейного оператора А: L → L совпадает с рангом этого оператора.

◄ Образ imA линейного оператора А представляет собой линейную оболочку системы векторов Ab₁, ..., Ab_n, где b₁, ..., b_n - некоторый базис линейного пространства L. Размерность линейного подпространства imA, представляющая собой ранг оператора, совпадает с максимальным количеством линейно независимых векторов в системе Ab₁, ... , Ab_n и равна максимальному количеству линейно независимых столбцов в матрице А, составленной из столбцов координат этих векторов. Но матрица А является матрицей оператора А. Значит, dim imA совпадает с рангом матрицы оператора А в указанном базисе. Поскольку понятие ранга линейного оператора не зависит от выбора базиса, то и ранг его матрицы в любом базисе один и тот же. ►

Замечание 4.2. Связь между линейными операторами и матрицами, вскрытая доказанными теоремами, позволяет дать геометрическую интерпретацию системе линейных алгебраических уравнений (СЛАУ). Если СЛАУ записать в матричной форме Ах = b, то матрицу А можно связать с некоторым линейным оператором А, а столбцы х и b интерпретировать как столбцы координат векторов x и b. Мы приходим к операторному уравнению, Ах = b, решение которого означает определение вектора х по его образу b. В частном случае b = 0 СЛАУ однородна, а решение операторного уравнения означает определение ядра оператора. Отметим, что тривиальное решение х = 0 однородной СЛАУ Ах = 0 соответствует нулевому вектору, всегда входящему в ядро оператора.

1. Линейные операции над векторами

2. Базис. Cкалярное произведение

3. Векторное и смешанное произведения векторов

4. Декартова система координат. прямая на плоскости

5. Плоскость в пространстве

6. Прямая в пространстве

7. Кривые второго порядка — I

8. Кривые второго порядка — II

9. Поверхности второго порядка

10. Матрицы и операции с ними

11. Обратная матрица

12. Ранг матрицы

13. Системы линейных алгебраических уравнений

14. Свойства решений однородных и неоднородных СЛАУ