Линейные оболочки и системы уравнений

Пусть L - n-мерное линейное пространство, в котором фиксирован некоторый базис е = (e₁ ... е_n) и выбраны векторы a₁, ..., a_k, b. Запишем разложение выбранных векторов по базису е:

a_j = ea_j, j = 1,k, b = eb,

где a_j = (a_1j ... a_nj)^T , j = 1,k, b = (b₁ ... b_n)^T - столбцы координат соответствующих векторов . Пусть А - матрица типа n × k, составленная из координатных столбцов векторов a₁, ..., а_k, а (A|b) - матрица, полученная из матрицы А добавлением справа еще одного столбца b.

Для вектора b возможны два случая:

1) вектор b принадлежит линейной оболочке span{a₁,..., a_k};

2) вектор b не принадлежит span{a₁,...,a_k}.

В первом случае добавление к системе векторов a₁, ..., a_k вектора b не приводит к расширению линейной оболочки системы и, следовательно,

dimspan{a₁,... ,а_k} = dimspan{a₁,... ,а_k,b}.

По теореме 2.6 заключаем, что RgA = Rg(A|b).

Во втором случае, наоборот, добавление вектора b к системе векторов a₁, ..., а_k приводит к расширению линейной оболочки, причем по теореме 2.5

dimspan{a₁,... ,а_k,b} = dimspan{a₁,... ,а_k} + 1,

так как

span{a₁,..., a_k, b} = span{a₁,..., a_k} ⊕ span{b}.

Следовательно, Rg(A|b) = RgA + 1.

Выясним теперь, что означают эти два случая "на координатном уровне". В первом случае условие b ∈ span{a₁,... ,a_k} означает существование разложения

х₁а₁ +... + x_ka_k = b (2.8)

с некоторыми действительными коэффициентами x₁, ..., x_k. Записывая это векторное равенство в координатной форме, получаем систему линейных алгебраических уравнений (СЛАУ)

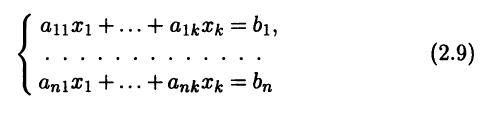
относительно переменных х = (х₁ ... x_k)^T, которая в матричной форме имеет вид Ах = b. Существование разложения (2.8) означает, что полученная система имеет решение. Во втором случае представление (2.8) невозможно, т.е. система (2.9) не имеет решений.

Итак, следующие четыре утверждения эквивалентны между собой:

- b ∈ span{a₁,...,a_k};

- dimspan{a₁,... ,а_k,b} = dimspan{a₁,...,а_k};

- Rg(A|b) = RgA;

- система Ах = b из n линейных алгебраических уравнений относительно k неизвестных совместна.

Эквивалентность последних двух утверждений составляет содержание теоремы Кронекера - Капелли [III], которая верна для произвольных СЛАУ. Отметим, что любая система из п ли-нейных алгебраических уравнений относительно к неизвестных может быть получена как результат проведенных рассуждений. Для этого достаточно в качестве векторов a₁, ..., a_k рассмотреть столбцы коэффициентов при неизвестных, а в качестве вектора b - столбец свободных членов. Все эти столбцы могут рассматриваться как n-мерные векторы в линейном арифметическом пространстве Rⁿ.

Таким образом, теорему Кронекера - Капелли можно переформулировать следующим образом: для того чтобы линейная оболочка системы векторов a₁, ..., а_k совпадала с линейной оболочкой расширенной системы a₁, ..., а_k, b, необходимо и достаточно, чтобы были равны размерности этих линейных оболочек.

Предположим, что квадратная СЛАУ Ах = b имеет решение при любом столбце b правых частей. Рассматривая столбцы матрицы А и столбец b как элементы a₁, ..., a_n, b n-мерного линейного арифметического пространства и записывая СЛАУ в векторной форме

x₁a₁ + x₂a₂ + ... + x_na_n = b,

заключаем, что линейная оболочка системы векторов a₁, ..., а_n совпадает со всем линейным пространством Rⁿ. Из этого следует, что ранг этой системы векторов равен размерности линейного пространства n, а так как в системе ровно n векторов, то она, согласно теореме 2.6, линейно независима. Другими словами, столбцы матрицы А линейно независимы, а матрица А является невырожденной (см. теорему о базисном миноре [III]).

Таким образом, если квадратная СЛАУ Ах = b имеет решение при любой правой части, то матрица А системы невырождег на, а решение системы при любой правой части единственно.

1. Линейные операции над векторами

2. Базис. Cкалярное произведение

3. Векторное и смешанное произведения векторов

4. Декартова система координат. прямая на плоскости

5. Плоскость в пространстве

6. Прямая в пространстве

7. Кривые второго порядка — I

8. Кривые второго порядка — II

9. Поверхности второго порядка

10. Матрицы и операции с ними

11. Обратная матрица

12. Ранг матрицы

13. Системы линейных алгебраических уравнений

14. Свойства решений однородных и неоднородных СЛАУ