Пересечение и сумма линейных подпространств

Пусть H₁, H₂ - линейные подпространства в линейном пространстве L.

Определение 2.2. Множество Н₁ ∩ Н₂ называют пересечением линейных подпространств Н₁ и Н₂

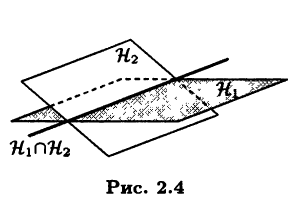
На рис. 2.4 видим, что два линейных подпространства, изображенные плоскостями, в пересечении дают прямую, также являющуюся представлением некоторого линейного подпространства (см. пример 2.1).

Теорема 2.1. Пересечение Н₁ ∩ Н₂ двух линейных под-пространств Н₁ и Н₂ в линейном пространстве L является линейным подпространством в L.

◄ Проверим, выполняется ли условие 1) определения 2.1. Если векторы x₁ и x₂ принадлежат Н₁ ∩ Н₂ то каждый из этих векторов принадлежит как Н₁ так и H₂. Поскольку Н₁ - линейное подпространство, то, согласно определению 2.1, заключаем, что вектор x₁ + x₂, павный сумме векторов этого линейного подпространства, тоже принадлежит Н₁. Аналогично х₁ + x₂ ∈ H₂ так как каждое из слагаемых является элементом линейного подпространства H₂ Следовательно, x₁ + x₂ ∈ Н₁ ∩ Н₂.

Проверим условие 2) определения 2.1. Выберем произвольный вектор х ∈ Н₁ ∩ Н₂. Тогда х ∈ Н₁ и х ∈ Н₂. Так как H₁ является линейным подпространством, то произведение элемента х этого линейного подпространства на произвольное действительное число λ принадлежит Н₁. Но совершенно аналогично вектор λх принадлежит и H₂. Поэтому λх ∈ Н₁ ∩ Н₂.

Итак, оба условия определения 2.1 выполнены. Следовательно, Н₁ ∩ Н₂ является линейным подпространством. ►

Определение 2.3. Множество Н₁ + Н₂ всех векторов х вида х = х₁ + x₂, где x₁ ∈ Н₁, x₂ ∈ H₂ называют суммой линейных подпространств H₁ и H₂.

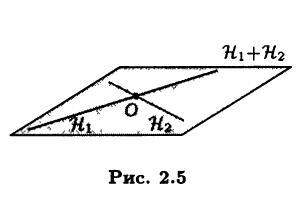
На рис. 2.5 линейные подпространства Н₁ и Н₂ представлены несовпадающими прямыми, проходящими через фиксированную точку О. Их сумма представляется плоскостью, содержащей обе прямые.

Теорема 2.2. Сумма линейных подпространств данного линейного пространства является линейным подпространством в том же линейном пространстве.

◄ Рассмотрим два вектора v и w из множества Н₁ + Н₂. Согласно определению 2.3, имеют место представления

v = x₁ + x₂, w = y₁ + y₂,

где векторы x_i, у_i принадлежат H_i, i = 1,2. Складывая эти равенства, получаем

v + w = (x₁ + y₁) + (x₂ + y₂).

Сумма x₁ + y₁ векторов x₁ и y₁ линейного подпространства Н₁ принадлежит H₁. Точно так же сумма x₂ + у₂ векторов x₂ и у₂ линейного подпространства Н₂ принадлежит Н₂. Поэтому вектор v + w принадлежит множеству H₁ + Н₂.

Условие 2) определения 2.1 проверяется аналогично. Произвольный вектор v ∈ H₁ + Н₂ имеет представление v = x₁ + x₂, где x₁ ∈ H₁, x₂ ∈ H₂. Для любого действительного числа λ получаем равенства

λv = λ(x₁ + x₂) = λx₁ + λx₂.

Так как вектор λx₁ принадлежит H₁, а вектор λх₂ - H₂, то вектор λv является элементом множества H₁ + H₂.

Мы доказали, что множество H₁ + Н₂ замкнуто относительно линейных операций объемлющего линейного пространства и поэтому, согласно определению 2.1, оно является линейным подпространством. ►

Пример 2.6. Рассмотрим две однородные системы линей-ных алгебраических уравнений

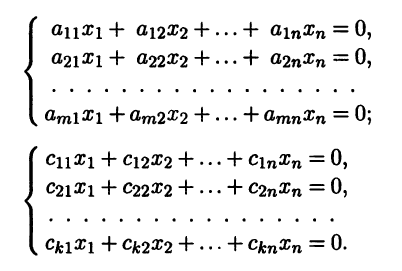
Множества решений этих систем представляют собой линейные подпространства H₁ и Н₂ линейного арифметического пространства Rⁿ. Объединив обе системы в одну, получим новую однородную систему, множеством решений которой будет линейное подпространство Н₁ ∩ Н₂.

Пример 2.7. Рассмотрим две системы векторов е₁,..., е_k и f₁, ..., f_l в некотором линейном пространстве L. Линейные дболочки этих систем представляют собой линейные подпространства Н₁ = span{e₁,...,е_k} и H₂ = span{f₁,..., f_l} в L. Если мы объединим обе системы в одну, то у новой, объединенной системы линейной оболочкой будет линейное подпространство H₁ + H₂. В самом деле, любой вектор х ∈ Н₁ + Н₂ разлагается в сумму х = х₁ + x₂, где х₁ ∈ H₁, x₂ ∈ H₂. Векторы х₁ и x₂ представляются в виде линейной комбинации, первый - векторов е₁, ... , e_k, второй - векторов f₁, ..., f_l. Значит, их сумма представляется линейной комбинацией векторов е₁, ... ,e_k , f₁, ..., f_l т.е. - вектор х принадлежит span{e₁,...,e_k,f₁,..,f_l}. Предположим теперь, что вектор x принадлежит указанной линейной оболочке, т.е. имеет место представление

x = α₁e₁ + ... + α_ke_k + β₁f₁ + ... +β_lf_l.

Положив

x₁ = α₁e₁+ ... + α_ke_k,

x₂ = β₁f₁+ ... + β_lf_l

приходим к представлению х = х₁ + x₂, в котором х₁ ∈ H₁, x₂ ∈ H₂. Значит, х ∈ H₁ + H₂.

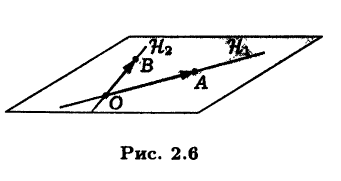
Пример 2.8. Линейное подпространство из примера 2.5, являющееся линейной оболочкой span{OA, OB}, можно представить как сумму подпространств H₁ = span{OA} и H₂ = span{OB} (рис. 2.6).

1. Линейные операции над векторами

2. Базис. Cкалярное произведение

3. Векторное и смешанное произведения векторов

4. Декартова система координат. прямая на плоскости

5. Плоскость в пространстве

6. Прямая в пространстве

7. Кривые второго порядка — I

8. Кривые второго порядка — II

9. Поверхности второго порядка

10. Матрицы и операции с ними

11. Обратная матрица

12. Ранг матрицы

13. Системы линейных алгебраических уравнений

14. Свойства решений однородных и неоднородных СЛАУ