Обусловленность квадратных матриц

При решении любой математической задачи важную роль играет вопрос существования и единственности решения. Но положительный ответ на этот вопрос еще не гарантирует достоверности практических результатов, которые получены в результате решения математической задачи. Поясним это подробнее.

При постановке математической задачи, как правило, име-ются параметры, которые не фиксированы и могут принимать произвольные значения из некоторых интервалов. В качестве таких параметров могут рассматриваться данные измерений, результаты решения каких-то других задач, результаты экс-пертных оценок и т.п., которые задаются приближенно. Если при каждом допустимом наборе значений параметров (входных данных математической задачи) задача имеет решение, и притом единственное, то возникает зависимость решения от указанных параметров.

Результатом решения математической задачи является вычисление на основе входных данных некоторого набора числовых значений — выходных данных математической задачи. Как входные, так и выходные данные можно рассматривать в качестве элементов соответствующих нормированных пространств. Это позволяет сравнивать между собой различные варианты входных (выходных) данных и оценивать степень их близости, что приводит к понятию непрерывной зависимости решения задачи от входных данных.

Пусть х, x₀ ∈ R^m представляют собой векторы входных данных некоторой математической задачи, а y, y₀ ∈ R^m — со-ответствующие этим входным данным решения, или выходные данные. Скажем, что решение задачи непрерывно зависит от входных данных, если для любого x₀ и для любого ε > 0 существует такое δ > 0, что при ||x — x₀|| < δ имеем ||у — y₀|| < ε, где ||·|| — некоторая норма в R^m.

Математическую задачу называют корректной или корректно поставленной, если ее решение существует, един-ственно и непрерывно зависит от входных данных. Бели одно из трех условий нарушается (решение неединственно, не существует или нарушается требование непрерывной зависимости от входных данных), то говорят о некорректной математической задаче.

Понятие корректной задачи легко конкретизировать для системы линейных алгебраических уравнений (СЛАУ) с невырожденной матрицей. Напомним, СЛАУ Ах = b с квадратной матрицей А порядка n имеет единственное решение тогда и только тогда, когда матрица А невырождена [III]. Входными данными задачи решения СЛАУ следует считать элементы ее матрицы и правые части уравнений.

Столбец неизвестных х и столбец правых частей b СЛАУ Ах = Ъ можно трактовать как векторы n-мерного линейного арифметического пространства Rⁿ, в котором задана некоторая норма ||·||. Этой норме соответствует индуцированная норма матрицы, для которой будем использовать то же обозначение ||·||. Изменение входных данных означает, что наряду со СЛАУ Ах = b с решением надо рассмотреть другую возмущенную систему ^~Ах = ^~b с матрицей ^~А = А + ΔА и столбцом правых частей b = b + Δb, которая отличается от исходной системы возмущением матрицы системы ΔА и возмущением столбца правых частей ΔЬ. Решением возмущенной системы будет некоторый столбец ^~x, который отличается от х на столбец Δх = ^~х — x, называемый возмущением решения. Величины ||ΔА||, ||Δb|| и ||Δx|| можно интерпретировать как абсолютные погрешности соответственно матрицы системы, правой части и решения, если компоненты исходной системы рассматривать как точные. При этом относительные погрешности будут выражаться формулами

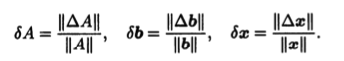
Корректность задачи решения СЛАУ Ах = b с квадратной невырожденной матрицей заключается в том, что малым от-носительным погрешностям матрицы системы и правой части отвечает малая относительная погрешность решения системы. Чтобы показать, что это действительно так, нужно относительную погрешность решения оценить с помощью относительных погрешностей матрицы и правой части.

Определение 11.1. Для квадратной невырожденной матрицы А величину

c(A) = ||A||||A^-1|| (11.1)

называют ее числом обусловленности.

Число обусловленности матрицы всегда положительно и зависит от заданной нормы матриц. Эта характеристика имеет следующие свойства.

Свойство 11.1. Для любой невырожденной матрицы А число ее обусловленности совпадает с числом обусловленности обратной матрицы А^-1:

c(A) = c(A^-1).

с(А^-1) = ||A^-1|| ||(A^-1)^-1|| = |A^-1|| ||А|| = с(А).

Свойство 11.2. Бели норма матриц кольцевая, то с(АВ) ≤ с(А)с(B).

Согласно свойствам обратной матрицы, (АВ)^-1 = B^-1А^-1, а согласно условию, что норма кольцевая, ||АВ|| ≤ ||А||||В||. Поэтому

с(АВ) = ||AB|| ||(AВ)^-1| ≤ ||A|| ||В|| ||В^-1|| ||А^-1|| = (||A||||A^-1||)(||В|||||B^-1||)=с(А)с(В).

Свойство 11.3. Если матричная норма кольцевая, то с(А) ≥ 1 для любой невырожденной матрицы А.

Для единичной матрицы Е, согласно равенству ЕЕ = Е и свойству 11.2, получаем

с(Е) = с(ЕЕ) ≤ с(Е) с(Е).

Так как с(Е) > 0, то, сокращая в неравенстве на с(Е), имеем с(Е) ≥ 1.

Для невырожденной матрицы А существует обратная матрица A^-1, при этом AA^-1 = Е. Согласно свойствам 11.1 и 11.2, заключаем, что

1 ≤ с(Е) = с(АА^-1) ≤ с(A) c(A^-1) = (с(A))².

Значит, с (А) ≥ 1, так как число обусловленности матрицы неотрицательное.

Свойство 11.4. Если ||·|| — спектральная норма, то число обусловленности симметрической матрицы А равно

с(А) = |λmax|/|λmin|,

где λmах, λmin — ее собственные значения, соответственно наибольшее и наименьшее по абсолютной величине.

Спектральная норма симметрической матрицы равна макси-мальной из абсолютных величин |λ_i| ее собственных значений. Действительно, если симметрическая матрица имеет порядок n, то в Rⁿ существует ортонормированный базис е₁,..., е_n из ее собственных векторов. Пусть соответствующие им собствен-ные значения связаны неравенствами |λ₁| ≥ |λ₂| ≥ ... ≥ |λ_n|. То гда для любого вектора х = α₁е₁ +... + α_nе_n имеем

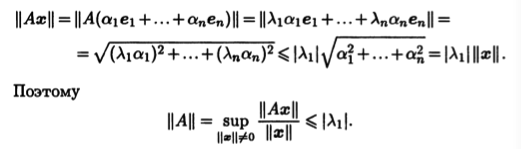
Но на самом деле в приведенном неравенстве должен стоять знак равенства, так как для х = е₁ имеем

||Ax||/||x|| = ||λе₁е₁||/||е₁|| = |λе₁|

Отметим, что если λ — собственное значение невырожден-ной матрицы А, то λ^-1 — собственное значение матрицы А^-1, так как равенство Ах = λх, х ≠ 0, равносильно равенству А^-1х = λ^-1x. Кроме того, если А — симметрическая матрица, т.е. А^T = А, то и А^-1 — симметрическая матрица, так как (A^-1)^T = (А^T)^-1 = А^-1 Поэтому, если λmах и λmin — соответственно наибольшее и наименьшее по абсолютной величине собственные значения матрицы А, то ||A|| = |λmах|, ||A^-1|| = |λ^-1min|. Следовательно, с(А) = ||А||||A^-1|| = |λmax| |λ^-1min|.

Число обусловленности матрицы А в значительной степени определяет чувствительность СЛАУ Ах = Ь к погрешностям в коэффициентах матрицы и в правых частях уравнений: чем больше это число, тем выше погрешность решения при данном уровне погрешностей входных данных. Эту связь показывает следующая теорема.

Теорема 11.1. Если матрица А невырождена и

||ΔA||<||A^-1||^-1 , (11.2)

где ||·|| — произвольная кольцевая норма матриц, то матрица ^~А = А + ΔА тоже невырождена и верна следующая оценка для относительной погрешности решения

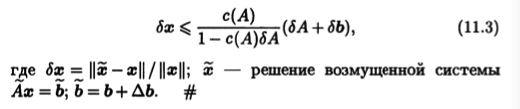
Замечание 11.1. Если выполняется неравенство (11.2), то

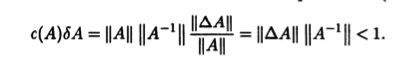
В этом случае в правой части неравенства (11.3) деления на нуль нет, и она положительная.

1. Линейные операции над векторами

2. Базис. Cкалярное произведение

3. Векторное и смешанное произведения векторов

4. Декартова система координат. прямая на плоскости

5. Плоскость в пространстве

6. Прямая в пространстве

7. Кривые второго порядка — I

8. Кривые второго порядка — II

9. Поверхности второго порядка

10. Матрицы и операции с ними

11. Обратная матрица

12. Ранг матрицы

13. Системы линейных алгебраических уравнений

14. Свойства решений однородных и неоднородных СЛАУ