Сопряженное пространство

Определение 10.1. Отображение f: L → R которое опрелено на линейном пространстве L и принимает действительные значения, называют линейной функцией (также линейной формой, линейным функционалом), если оно у довлев творяет двум условиям:

а) f(x + у) = f(x) + f(x), х,у ∈ L;

б) f(λx) = λf(x), х ∈ L,λ ∈ R.

Сравнив данное определение с определением 4.1 линейного оператора, увидим много общего. Бели рассматривать множе-ство действительных чисел как одномерное линейное простран-ство, то можно сказать, что линейная функция — это линейный оператор, пространство образов которого одномерно.

Выберем в линейном пространстве L некоторый базис е = (e₁ ... е_n). Тогда для любого вектора х ∈ L с координатами х = (х₁; ... х_n)^T

f(x) = f(x₁e₁ +... + x_ne_n) = xi₁f(e₁) + ... + x_nf(e_n) = a₁x₁ + ... + a_nx_n = ax,

где a = (ai ... an), a* = /(e*), i = 1, n. Поэтому линейная функция однозначно определяется своими значениями на базисных векторах. Наоборот, если функция /(ж) через координаты х вектора ж выражается в виде /(ж) = аж, то эта функция ли-нейная, а строка а составлена из значений этой функции на базисных векторах. Таким образом, между множеством линей-ных форм, заданных на линейном пространстве £, и строками длины п установлено взаимно однозначное соответствие.

Линейные формы можно складывать и умножать на действительные числа согласно правилам:

(f + g)(x)=f(x)+g(x), (λf)(x) = λf(x).

Введенные таким способом операции превращают множество линейных форм в пространстве L в линейное пространство. Это линейное пространство называют сопряженным пространством по отношению к линейному пространству L и обозначают L*.

Опираясь на базис е, выбранный в пространстве L, построим базис в сопряженном пространстве L*. Для каждого вектора e_i из базиса е рассмотрим линейную форму fⁱ, для которой fⁱ(е_i) = 1 и fⁱ(е_j)= 0 для всех векторов e_j, кроме е_i. Мы получим систему линейных форм f1, ..., /” е С*. Покажем, что это линейно независимая система. Пусть некоторая линейная комбинация этих форм равна нулевой линейной форме / = aif1 +... + anfn = 0. Форма / на всех базисных векторах принимает нулевые значения. Но

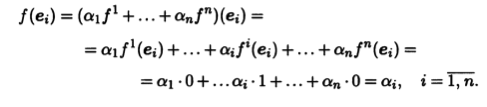
Нулевые значения f на базисных векторах эквивалентны равенствам α_i = 0, i = 1,n, и поэтому система линейных форм f¹, ..., fⁿ линейно независима.

Система линейных форм f¹, ..., fⁿ является базисом в сопряженном пространстве. Действительно, так как это линейно независимая система линейных форм, то достаточно доказать, что любая линейная форма из L* является их линейной комбинацией. Выберем произвольную линейную форму f из L* и пусть а₁ ..., а_n — значения формы f на базисных векторах. Эти значения однозначно определяют линейную форму. Но линейная комбинация f' = a₁f_i +... + a_nf_n также является линейной формой, которая на базисных векторах принимает те же значения a₁, ..., а_n. Значит, эти две линейные формы совпадают, и мы получаем равенство f = f' = a₁f¹ +... + a_nfⁿ, т.е. разложение произвольно выбранной линейной формы по системе форм f¹, ..., fⁿ

Приведенное рассуждение показывает, что сопряженное пространство L* имеет ту же размерность, что и L. Построенный нами базис f¹, ..., fⁿ зависит от выбора базиса е в пространстве L.

Определение 10.2. Базисы e₁, ..., е_n и f¹, ..., fⁿ линейного пространства L и сопряженного пространства L* называют биортогоналъными, или взаимными, если

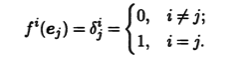
Если базисы e₁, ..., е_n и f¹, ..., fⁿ взаимны, то координатами произвольной формы f в базисе f¹, ..., fⁿ являются значения этой формы на векторах взаимного базиса e₁, ..., е_n. При совместном рассмотрении линейного пространства L и сопряженного пространства L* элементы каждого из этих пространств называют векторами, но элементы сопряженного пространства L* именуют ковариантными векторами (ковекторами), а элементы из линейного пространства L — контравариантными векторами (или просто векторами). Координаты тех и других определяются преимущественно во взаимных базисах, при этом у координат контравариантных векторов индекс ставится вверху, а у ковариантных — внизу.

На запись f(x) можно смотреть двояко. Зафиксировав форму f, мы варьируем вектор x, получая всевозможные значения линейной формы. Но если мы зафиксируем вектор х и будем варьировать линейную форму f, то получим функцию, определенную на сопряженном пространстве L*. Нетрудно убедиться, что эта функция линейная, так как, согласно определению сум-мы линейных форм и произведения линейной формы на число,

(f + g)(x) = f(x) + g(x), (λf)(x) = λf(x)•

Итак, каждому вектору x ∈ L соответствует линейная форма на сопряженном пространстве L, или элемент двойного сопряженного пространства (L*)* = L**. Мы получаем отображение φ: L → L**. Несложно убедиться, что это отображение линейно и что оно инъективно. Из инъективности следует, что dimimφ = dimL = n. Но сопряженное пространство L* имеет ту же размерность, что и L, a dimL** = dimL* = dimL. Таким образом, размерность линейного подпространства imφ в L** совпадает с размерностью всего двойного сопряженного пространства. Значит, imφ = L** и отображение φ является изоморфизмом. Обратим внимание, что этот изоморфизм не связан с выбором какого-либо базиса. Поэтому естественно отождествить линейные формы, заданные на L*, с элемента-ми пространства L. Это означает, что двойное сопряженное пространство совпадает с исходным линейным пространством: L** = L. Если L* является сопряженным к L, то и L является сопряженным к L*.

Взаимность линейного пространства и сопряженного к нему пространства указывает на симметричность связи между векторами и ковекторами. Поэтому вместо записи f(x) более удобно использовать другую форму записи, симметричную: (f,x). Линейные формы мы также будем теперь обозначать полужирным курсивом: (f,x). Принятое обозначение похоже на обозначение скалярного произведения, но в отличие от последнего аргументы в новом обозначении берутся из разных пространств. Саму запись (f, x) можно рассматривать как запись отображения, определенного на множестве L*×L, которое паре из ковектора и вектора ставит в соответствие действительное число. При этом указанное отображение линейно по каждому из аргументов.

Теорема 10.1. Пусть b и с — два базиса n-мерного линейного пространства L,U — матрица перехода из b в с. Базисы b* и с* сопряженного пространства L*, взаимные с базисами b и с соответственно, связаны между собой соотношениями

c* = b*(U^T)^-1 Ь* =c*U^T

Координатами f^c = (f^c₁ ... f^c_n) линейной формы f в базисе с* являются значения этой формы на векторах базиса с = (c₁ ... c_n). Выясним, как связаны координаты формы f в двух базисах с* и b*.

Базисы b и с связаны между собой при помощи матрицы' перехода матричным соотношением с = bU (см. 1.8). Это соотношение представляет собой равенство строк длины n, составленных из векторов. Из равенства строк векторов следует равенство строк значений линейной формы f на этих векторах:

((f,c₁) ... (f,c_n)) = ((f,b₁) ... (f,b_n))U,

или

f^c = f^bU,

где f^b и f^c — обозначения строк координат формы f в базисах Ь* и с* соответственно. Транспонировав это равенство, мы получим принятую форму связи координат элементов линейного пространства, в которой координаты записываются по столбцам:

(f^c)^T = U^T(f^b)^T.

Это соотношение означает, что матрица U^T является матрицей перехода из базиса с*, играющего в формуле роль старого, в базис b*, играющий роль нового. Следовательно, b* = c*U^T, откуда умножением на матрицу (U^T)^-1 получаем с* = b*(U^T)^-1. ►

Бели линейное пространство L евклидово, то скалярное про-изведение порождает изоморфизм между L и l*, не зависящий от базиса, который позволяет отождествить евклидово про-странство с его сопряженным. Действительно, для любого вектора a ∈ L отображение x → (а,x) представляет собой линейную форму в L, так как скалярное произведение линейно по второму из своих аргументов. Возникает отображение ψ, которое вектору a ∈ L ставит в соответствие линейную форму f_a(x) — (а,x). Это отображение линейно в силу свойств скалярного произведения и инъективно. Инъективность следует из того, что если (а,x) = 0 для любого x ∈ L, то и (a,а) = 0, т.е. a = 0. Так как линейные пространства L и L* конечномерны и имеют одинаковые размерности, отображение ∈ биективно и реализует изоморфизм этих пространств. Итак, для евклидова пространства L* = L. В этом смысле евклидово пространство есть " самосопряженное " пространство.

1. Линейные операции над векторами

2. Базис. Cкалярное произведение

3. Векторное и смешанное произведения векторов

4. Декартова система координат. прямая на плоскости

5. Плоскость в пространстве

6. Прямая в пространстве

7. Кривые второго порядка — I

8. Кривые второго порядка — II

9. Поверхности второго порядка

10. Матрицы и операции с ними

11. Обратная матрица

12. Ранг матрицы

13. Системы линейных алгебраических уравнений

14. Свойства решений однородных и неоднородных СЛАУ