Критерий Сильвестра

Квадратичные формы подразделяют на различные типы в зависимости от множества их значений.

Определение 8.3. Квадратичную форму f(x) = х^TАх, х = (х₁ ... х_n)^T , будем называть:

- положительно (отрицательно) определенной, если для любого ненулевого столбца х выполняется неравенство f(x) > 0 (f(x) < 0);

- неотрицательно (неположительно) определенной, если f(x) ≥ 0 (f(x) ≤ 0) для любого столбца х, причем существует ненулевой столбец х, для которого f(x) = 0;

- знакопеременной (неопределенной), если существуют такие столбцы x и у, что f(x) > 0 и f(y) < 0.

Пример 8.6. Рассмотрим четыре квадратичные формы от трех переменных:

f₁(x₁,x₂,x₃) = x²₁ + x²₂ + x²₃,

f₂(x₁,x₂,x₃) = x²₁ + x²₂,

f₃(x₁,x₂,x₃) = x²₁ - x²₂ + x²₃,

f₃(x₁,x₂,x₃) = x₁x₂.

Квадратичная форма f₁ положительно определена, так как представляет собой сумму трех квадратов и потому принимает только положительные значения, если переменные одновременно не обращаются в нуль. Квадратичная форма f₂ неотрицательно определена: будучи суммой двух квадратов она не принимает отрицательных значений, но при х₁ = x₂ = 0 и х₃ ≠ 0 она принимает нулевые значения. Квадратичные формы f₃ и f₄ знакопеременны. Первая из них положительна при х = (1 0 0) и отрицательна при х = (0 1 0)^T . Вторая положительна при x = (1 1 0)^T и отрицательна при х = (1 -1 0)^T. Квадратичные формы f₂ и f₄ являются вырожденными, так как ранг каждой из них равен двум. #

Как следует из определения 8.3, тип квадратичной формы зависит только от множества значений, которые она принимает, но не зависит от переменных, в которых она записана. Поэтому, представив квадратичную форму в каноническом виде, сразу получаем следующие критерии для типа квадратичной формы в зависимости от множества собственных значений ее матрицы.

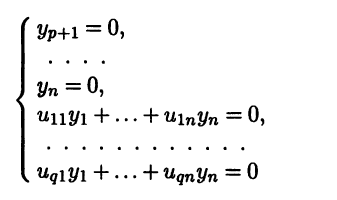
Хотя эта таблица дает удобную характеристику типам квадратичных форм, ее использование для определения типа конкретной квадратичной формы связано с вычислением соб-ственных значений матрицы. А это достаточно трудоемкая операция. На самом деле во многих случаях тип квадратичной формы можно определить, не вычисляя собственных значений ее матрицы. Метод состоит в вычислении и проверке знаков некоторых миноров матрицы квадратичной формы. Введем следующие обозначения.

Пусть матрица квадратичной формы f(x) = х^TАх имеет вид

где a_ij = a_ji, i,j = 1,n. Рассмотрим угловые миноры этой матрицы (которые также называют главными минорами):

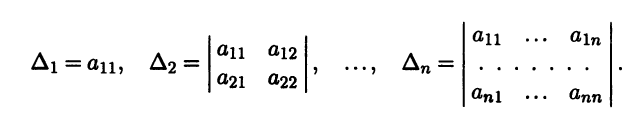
Как видим, угловой минор порядка k расположен на пересечении первых k строк и первых k столбцов матрицы. Угловой минор максимального, n-го порядка представляет собой определитель матрицы.

Теорема 8.6 (критерий Сильвестра). Для того чтобы квадратичная форма от n переменных была положительно определена, необходимо и достаточно, чтобы выполнялись неравенства Δ₁ > 0, Δ₂ > 0, Δ₃ > 0, ..., Δ_n > 0.

◄ Необходимость. Если квадратичная форма положительно определена, то в ее каноническом виде все коэффициенты должны быть положительны. Значит, и определитель матрицы квадратичной формы канонического вида положителен. Невырожденное преобразование квадратичной формы не меняет знака определителя, так как, согласно формуле преобразования (8.4), det(U^TAU) = (detU)²detА. Поэтому определитель матрицы исходной канонической формы тоже положителен, т.е. Δ_n > 0

Если квадратичная форма f(x₁, ... ,х_n) от _n переменных положительно определена, то квадратичная форма f_k(x₁,... ,x_k) = f(x₁,...,x_k,0,...,0) от k переменных также положительно определена и, следовательно, определитель ее матрицы положителен. Но этот определитель совпадает с Δ_k, т.е. Δ_k > 0 при k = 1,n.

Достаточность. Используем метод математической индукции по количеству n переменных квадратичной формы. При n = 1 утверждение очевидно. Пусть утверждение верно для всех квадратичных форм от k переменных, k ≤ n - 1. Рассмотрим произвольную квадратичную форму f(x) с матрицей А = (a_ij) в базисе е = (e₁ ... е_n), у которой все угловые миноры положительны. Квадратичная форма f_n-1(x₁,...,x_n-1) = f(x₁,... ,x_n-1,0) от n - 1 переменных определена на линейном подпространстве H_n-1= span{e₁,...,e_n-1} и имеет матрицу, совпадающую с матрицей минора Δ_n-1. Так как все угловые миноры для Δ_n-1, они же угловые миноры матрицы А, положительны, согласно предположению математической индукции квадратичная форма f_n-1 является положительно определенной. Заменой базиса (e₁ ... e_n-1) подпространства H_n-1 новым базисом (f₁ ... f_n-1) мы можем привести квадратичную форму f_n-1 к диагональному виду:

f_n-1(x) = λ₁x²₁ + ... + λ_n-1x²_n-1, λ_i > 0, i = 1,n-1. (8.9)

В базисе (f₁ ... f_n-1 e_n) квадратичная форма f(x) имеет вид

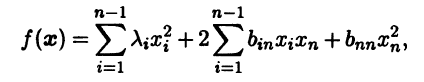
так как при х_n = 0 она совпадает с квадратичной формой f_n-1. Преобразуем последнее выражение для f(x), выделяя квадраты по переменным х₁, х_n-1:

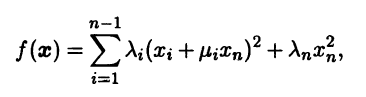
где μ = b_in/λ_i, i = 1,n-1, λ_n = b_nn - λ₁μ²₁ - ... - λ_n-1μ²_n-1 Выполнив линейную замену переменных х'_i = х_i + μ_ix_n, i = 1,n-1, х'_n = х_n с невырожденной матрицей, приходим к квадратичной форме канонического вида

f(x) = λ₁(x'₁)² + ... + λ_n(x'_n)², (8.10)

в которой, согласно (8.9), коэффициенты λ₁, ..., λ_n-1 положительны. У определителя матрицы квадратичной формы знак не зависит от выбора базиса. Поэтому в представлении (8.10) имеем λ₁... λ_n-1λ_n > 0, так как Дп > 0. Отсюда следует, что Ап > 0, так как все остальные коэффициенты А* положительны. Таким образом, в представлении (8.10) все коэффициенты положительны и квадратичная форма f(x) положительно определена. ►

Следствие 8.1. Для того чтобы квадратичная форма п переменных была отрицательно определена, необходимо и достаточно, чтобы выполнялись неравенства -Δ₁ > 0, Δ₂ > 0, -Δ₃ > 0, ..., (-1)ⁿ Δ_n > 0 (знаки угловых миноров чередуются начиная с минуса).

◄ Если квадратичная форма f(x) отрицательно определена, то квадратичная форма -f(x) положительно определена, и наоборот. Матрицей квадратичной формы -f(x) является матрица -А, противоположная матрице А квадратичной формы f(x). Согласно критерию Сильвестра, для положительной определенности квадратичной формы -f(x) необходимо и достаточно, чтобы все угловые миноры Δ'_r, r = 1,n, матрицы -А были положительны. Но при умножении матрицы А на число - 1 все ее элементы умножаются на это число и поэтому Δ'_r = (-1)^r Δ_r, где Δ_r - угловой минор порядка r матрицы А. Таким образом, квадратичная форма -f(x) положительно определена тогда и только тогда, когда выполнены неравенства (-1)^r Δ_r > 0, r = 1,n, и это условие эквивалентно тому, что квадратичная форма f(x) отрицательно определена. ►

Следствие 8.2. Невырожденная квадратичная форма знакопеременна тогда и только тогда, когда для матрицы квадратичной формы выполнено хотя бы одно из условий:

- один из угловых миноров равен нулю;

- один из угловых миноров четного порядка отрицателен;

- два угловых минора нечетного порядка имеют разные знаки.

◄ Невырожденная квадратичная форма может быть либо положительно определенной, либо отрицательно определенной, либо знакопеременной - в зависимости от знаков коэффициентов в ее каноническом виде. Если имеется нулевой угловой минор или один из угловых миноров четного порядка отрицателен, то, согласно теореме 8.6 и следствию 8.1, эта квадратичная форма не является ни положительно, ни отрицательно определенной. То же можно утверждать и в случае, когда есть два угловых минора нечетного порядка с разными знаками. Значит, в этих случаях квадратичная форма знакопеременная. ►

Критерий Сильвестра и его следствия показывают, что тип квадратичной формы полностью определяется свойствами ее матрицы. Поэтому термины, введенные определением 8.3, можно перенести на симметрические матрицы. В частности, симметрическую матрицу А называют положительно (отрицательно) определенной и пишут А > 0 (А < 0), если положительно (отрицательно) определена соответствующая квадратичная форма. Согласно теореме 8.6 и ее следствиям, симметрическая матрица положительно определена, если все ее угловые миноры положительны. Симметрическая матрица отрицательно определена, если у ее угловых миноров знаки чередуются начиная со знака минус.

Следствие 8.3. Если симметрическая матрица положи-тельно определена, то все ее диагональные элементы положительны.

◄ Если А = (a_ij) - симметрическая положительно определенная матрица порядка n, то ее первый угловой минор положителен, т.е. а₁₁ = Δ₁ > 0. Воспользовавшись тем, что утверждение следствия верно для диагонального элемента а₁₁, докажем что и а_ii > 0 при i > 1. В квадратичной форме х^TАх, x = (x₁,...,x_n)^T сделаем замену переменных

х₁ = у_i, x_i = y₁, x_j = y_j при j ≠ 1,i.

В новых переменных матрица А' = (а'_ij) квадратичной формы такова, что а_ii = а'₁₁ > 0. ►

Рассмотрим примеры на применение критерия Сильвестра.

Пример 8.7. Квадратичная форма х^TАх от трех переменных с матрицей

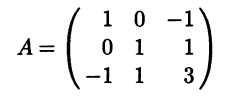
положительно определена, так как Δ₁ = Δ₂ = Δ₃ = 1 > 0.

Пример 8.8. Квадратичная форма х^TАх от трех переменных с матрицей

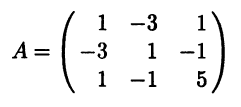
является знакопеременной, так как она невырождена (Δ₃ ≠ 0) и Δ₁ = 1 > 0, а Δ₂ = -8 < 0.

Пример 8.9. Квадратичная форма 2x₁x₂ от двух переменных является знакопеременной, так как она невырождена (Δ₂ = -1 ≠ 0), a Δ₁ = 0.

Пример 8.10. Квадратичная форма f(x₁, x₂, x₃, x₄) = 4х₁х₃ + 2x₂x₄ + х²₄ имеет угловые миноры Δ₁ = Δ₂ = Δ₃ = 0, Δ₄ = 4 и, согласно следствию 8.2, является знакопеременной. В этом можно убедиться, используя несложное преобразование вида квадратичной формы:

f(x₁,x₂,x₃,x₄) = (х₁ + x₃)² - х²₂ - (х₁ - x₃)² + (x₂ + x₄)².

Дополнение 8.1. Билинейные формы

Функцию b(х,у) от двух переменных, определенную в линейном пространстве L, называют билинейной формой, если эта функция линейна по каждому из своих аргументов, т.е. для любых действительных α и β и любых векторов x,y,z ∈ L выполняются равенства

b(αx + βy,z) = αab(x,z) + βb(y,z),

b(x,αy + βz) = αb(x,y) + βb{x,z).

Пример 8.11. Частным случаем билинейной формы является скалярное произведение. Действительно, аксиомы в) и г) скалярного умножения означают, что скалярное произведение как функция от двух переменных линейно по первому аргументу, а в силу аксиомы а) скалярное произведение линейно и по второму аргументу. #

Выберем в n-мерном линейном пространстве L некоторый базис е = (e₁ ... е_n). Для билинейной формы b(х,у) обозначим b_ij = b(e_i,e_j), i,j = 1,n. Тогда для любых векторов х и у со столбцами координат х = (х₁ ... x_n)^T и у = (у₁ ... у_n)^T в базисе е

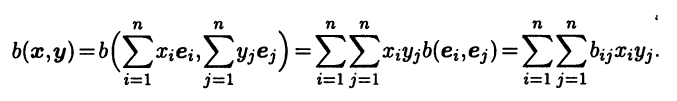
Используя квадратную матрицу В = (b_ij) порядка n, можем записать полученное представление в матричном виде:

b(х,у) = х^TВу. (8.11)

Матрицу В называют матрицей билинейной формы.

Тройное произведение, стоящее в правой части (8.11), нам уже встречалось (см., например, лемму на с. 185). Кстати, эта лемма показывает, что разным билинейным формам соответствуют разные матрицы. Таким образом, билинейная форма однозначно определяется своей матрицей в произвольно выбранном базисе. Кроме того, из леммы следует, что любая функция b, имеющая представление (8.11), является билинейной формой, и В является матрицей этой билинейной формы. Основываясь на этом, выясним, как изменяется матрица билинейной формы при изменении базиса.

Пусть билинейная форма b имеет в базисе b матрицу В_b, а в базисе е матрицу В_e. Обозначим через U матрицу перехода из базиса b в базис е. Тогда для любых двух векторов х, у со столбцами координат х_b, у_b в базисе b и х_e, у_e в базисе е имеем

b(x,y) = x^T_bA_by_b = (Ux_e)^TA_b(Uy_e) = x^T_e(U^TA_bU)y_e.

Сравнивая полученное представление с (8.11), делаем вывод, что матрица U^TA_bU является матрицей билинейной формы в базисе е, т.е.

А_e = U^TA_bU. (8.12)

Представление (8.11) билинейной формы в базисе похоже на запись (8.2) квадратичной формы в матричном виде. Кроме того, матрица билинейной формы преобразуется по тому же закону, что и матрица квадратичной формы (ср. (8.4) и (8.12)). Но матрица квадратичной формы симметрическая, в то время как матрица билинейной формы, вообще говоря, нет. Для того чтобы матрица билинейной формы b(x,у) в базисе е являлась симметрической, должны выполняться условия

b(e_i,e_j) = b(e_j,e_i), i,j = 1,n.

Если b(x,y) - билинейная форма, то функция b(х,х) в заданном базисе записывается в виде b(х, x) = х^TВх. Это матричное произведение представляет собой квадратичную форму от координат вектора х. Матрицей этой квадратичной формы является матрица А = 0,5(B + В^T). Матрицы билинейной и квадратичной форм совпадут, если матрица В билинейной формы симметрическая.

Пример 8.12. Функция b(x,y) = x₁y₁, заданная через координаты х = (x₁ x₂)^T и у = (y₁ y₂)^T векторов х и у в некотором базисе е двумерного линейного пространства, является билинейной формой с матрицей

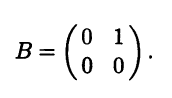
Соответствующая ей квадратичная форма имеет вид f(x) = x₁x₂ и матрицу

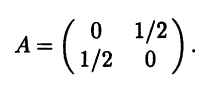
Отметим, что квадратичная форма f(x) порождается так-же и билинейной формой b_s(x,y) = 0,5x₁y₂ + 0,5x₂y₁, имеющей матрицу А.

Определение 8.4. Билинейную форму b(х,у) называют симметрической (кососимметрической), если b(х,у) = = b(у,х) (b(х,у) = -b(у,х)) для любых векторов х и у.

Пример 8.13. Примером симметрической билинейной формы является скалярное произведение. По существу, определение 3.1 говорит, что скалярное произведение - это билинейная симметрическая форма, порождающая положительно определенную квадратичную форму (последнее - содержание аксиомы г) скалярного произведения). #

Если в билинейной форме b(х,у) поменять местами переменные, то получим новую билинейную форму b'(x,у) = b(у,x), матрица которой будет транспонированной к исходной. Действительно, если в некотором базисе b(х,у) = х^TBy, то в том же базисе

b'(х,у) = b(у,х) = у^TВх = (y^TBx)^T = х^TВ^Tу,

так как у^TВх - это число и транспонирование его не меняет.

Если билинейная форма b(у,х) симметрическая, то перестановка аргументов не меняет ее. В этом случае b'(x, у) = b(х, у) и В^T = В, т.е. матрица симметрической билинейной формы является симметрической. Верно и обратное утверждение: если матрица В билинейной форма b(у,х) симметрическая, то и сама билинейная форма симметрическая. Это следует из равенств

b(х,у) = х^TВу = (х^TВу)^T = у^TВ^Tх = у^TВх = b(у,х).

Итак, для симметричности билинейной формы необходима и достаточна симметричность ее матрицы. Отметим, что если билинейная форма имеет симметрическую матрицу в одном базисе, то ее матрица будет симметрической и в любом другом базисе. Случай косимметрической билинейной формы аналогичен. Для того чтобы билинейная форма была кососимметрической, необходимо и достаточно, чтобы ее матрица в каком-либо базисе была кососимметрической.

Теорема 8.7. Для любой квадратичной формы f(x) существует, и притом единственная, симметрическая билинейная форма В(х,у), для которой f(x) = В(х,х) для любого вектора х.

◄ Выберем произвольный базис е и запишем в нем матрицу А квадратичной формы f(x). Билинейная форма b(х,у) с симметрической матрицей А в этом же базисе является сим-метрической и порождает квадратичную форму f(x) с той же матрицей А. Разные симметрические билинейные формы порождают квадратичные формы с разными матрицами. Значит, нмкакой квадратичной форме не могут соответствовать две различные симметрические билинейные формы. ►

Замечание 8.2. По квадратичной форме соответствующая ей билинейная форма легко восстанавливается, при этом не нужно прибегать к записи функций в каком-либо базисе. Рассмотрим функцию

b(x,у) = 0,5(f(x + y) - f(x) - f(y)).

Это билинейная симметрическая форма, что следует из ее записи в произвольном базисе:

b(х, у) = 0,5 ((x + y)^T А(х + у) - х^TАх - у^TАу) = 0,5 (х^TАу + у^TАх) = 0,5(х^TАу + (у^TАх)^T) = 0,5 (х^TАу + х^TА^Tу)/2 = х^TАу,

где А - матрица квадратичной формы f(x) в этом же базисе. При этом

b( х,х) - х^TАх = f(x).

Вопросы и задачи

1. Найдите ранг квадратичных форм от трех переменных: а) х² + у² + 2xz; б) 2ху + 2xz + 2yz; в) (х + у)² - (х - у - z)²; г) (x - y - 2z)².
2. Приведите к каноническому виду методом Лагранжа следующие квадратичные формы от трех переменных: а) х² + 2у² + 2xz + 2yz; б) 2ху + 2xz + 2yz; в) х² - у² + 2z² + 2 ху + 2xz.
3. Приведите к каноническому виду при помощи ортогонального преобразования следующие квадратичные формы от двух переменных: а) х² + ху + у²; б) ху; в) 2х² + 3у² + 2ху.
4. Какой ранг может иметь положительно определенная квадратичная форма от n переменных?
5. Определите тип следующих квадратичных форм от двух переменных: а) х² - ху + у²; б) 2ху; в) х² + 4ху + 4у².
6. Квадратичная форма от двух переменных имеет вид ах² + bху + су², т.е. является квадратным трехчленом относительно любой из переменных. Как тип квадратичной формы связан с дискриминантом этого квадратного трехчлена?
7. Выясните, являются ли положительно определенными следующие квадратичные формы от трех переменных: а) х² + у² - z² + 2ху + 2xz + 2yz; б) ху + xz + yz; в) х² + у² + z² + 2ху; г) х² + у² + z² + ху + xz + yz.

1. Линейные операции над векторами

2. Базис. Cкалярное произведение

3. Векторное и смешанное произведения векторов

4. Декартова система координат. прямая на плоскости

5. Плоскость в пространстве

6. Прямая в пространстве

7. Кривые второго порядка — I

8. Кривые второго порядка — II

9. Поверхности второго порядка

10. Матрицы и операции с ними

11. Обратная матрица

12. Ранг матрицы

13. Системы линейных алгебраических уравнений

14. Свойства решений однородных и неоднородных СЛАУ