Ортогональные преобразования квадратичных форм

Как мы установили (см. 8.2), матрица А квадратичной формы при переходе к новому базису изменяется по формуле А' = U^TAU, где U - матрица перехода. Бели рассматривается евклидово пространство, а старый и новый базисы выбраны ортонормированными, то матрица перехода U является ортогональной и мы имеем дело с ортогональным преобразованием квадратичной формы, т.е, преобразованием А' = U^TAU, в котором матрица U ортогональна.

Теорема 8.1. При ортогональном преобразовании квадратичной формы характеристическое уравнение ее матрицы не изменяется.

◄ Пусть А - матрица заданной квадратичной формы. При ортогональном преобразовании эта матрица изменяется по формуле А' = U^TAU, где U - ортогональная матрица. Согласно свойству 7.2, ортогональная матрица U имеет обратную, причем U^-1 = U^T. Поэтому А' = U^TAU = U^-1AU, И мы видим, что матрицы А' и А подобны. Согласно теореме 5.2, характеристи-ческие уравнения подобных матриц совпадают. ►

Теорема 8.2. Любую квадратичную форму ортогональным преобразованием можно привести к каноническому виду.

◄ Матрица А данной квадратичной формы является симме-трической. Но любая симметрическая матрица, согласно следствию 6.4, подобна диагональной, т.е. существует такая невырожденная матрица Р, что матрица А' = Р^-1 АР является диагональной. Нам надо лишь убедиться, что в качестве Р можно выбрать ортогональную матрицу. Тогда А' = Р^TАР и диагональная матрица А' является матрицей квадратичной формы, полученной из исходной при помощи ортогонального преобразования. Диагональный вид А' равнозначен каноническому виду квадратичной формы. Чтобы выяснить характер матрицы Р, нужно вспомнить теорему 6.5, из которой и было выведено упомянутое следствие 6.4.

Рассмотрим произвольное n-мерное евклидово пространство Ε (n - количество переменных в квадратичной форме) и некоторый ортонормированный базис b в этом пространстве. Матрица А является матрицей некоторого самосопряженного оператора А в базисе b. Согласно теореме 6.6, существует такой ортонормированный базис е, что матрица А' оператора А в этом базисе является диагональной. Согласно формуле преобразования матрицы линейного оператора, имеем А' = Р^-1АР (см. теорему 4.6), где Р - матрица перехода из базиса b в базис е. Так как оба базиса ортонормированные, матрица Р является ортогональной. ►

Теорема доказана, но подход, который мы использовали в доказательстве, позволяет сделать и другие выводы, о которых в формулировке теоремы речь не идет. Во-первых, диагональными элементами матрицы А' квадратичной формы канонического вида, получающейся в результате ортогонального преобразования, являются собственные значения матрицы А квадратичной формы. Из этого следует, что мы можем записать матрицу А' канонического вида, не находя соответствующего ортогонального преобразования.

Во-вторых, находя ортогональное преобразование, приводящее квадратичную форму к каноническому виду, мы фактически ищем базис из собственных векторов соответствующего самосопряженного оператора. Действительно, если квадратичная форма и самосопряженный оператор имели в исходном ортонормированием базисе одинаковую матрицу, то и в новом ортонормированием базисе их матрицы будут совпадать.

Мы предполагаем, что квадратичная форма представляет собой запись функции, заданной в евклидовом пространстве, через координаты вектора в некотором ортонормированном базисе. На самом деле такая интерпретация носит чисто вспомогательный характер, помогающий смотреть на процесс с геометрической точки зрения, но она никак не используется в самом алгоритме построения ортогонального преобразования. Достаточно лишь записать матрицу квадратичной формы и применить к этой матрице процедуру приведения к диаго-нальному виду (см. 7.4).

Проиллюстрируем на примерах процедуру практического вычисления ортогонального преобразования, приводящего квадратичную форму к каноническому виду.

Пример 8.4. Квадратичную форму f(x,у) = х²₁ - 4x₁x₂ от двух переменных мы приводили к каноническому виду методом Лагранжа (см. пример 8.3). Теперь попробуем привести ее к каноническому виду ортогональным преобразованием.

Матрица нашей квадратичной формы имеет вид

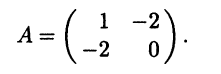
Найдем характеристическое уравнение этой матрицы:

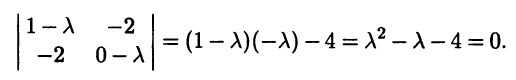
Вычисляем корни характеристического уравнения, они же собственные значения матрицы А:

λ_1,2 = (1 ± √17)/2.

Теперь можем записать канонический вид назраей квадратичной формы:

(1 + √17)/2 y²₁ + (1 + √17)/2 y²₂.

Пример 8.5. Найдем канонический вид квадратичной формы

f(x₁,x₂) = 5x²₁ + 8х₁x₂ + 5x²₂,

к которому она приводится ортогональным преобразованием, и укажем одно из таких ортогональных преобразований.

Квадратичная форма имеет матрицу

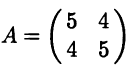
с характеристическим уравнением матрицы

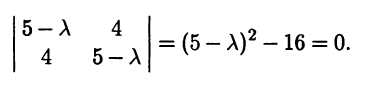
Собственными значениями матрицы квадратичной формы являются λ₁ = 1, λ₂ = 9, т.е. квадратичная форма приводится ортогональным преобразованием к каноническому виду

f(y₁,y₂) = y²₁ + 9y²₂.

Для построения ортогонального преобразования найдем собственные векторы матрицы рассматриваемой квадратичной формы. Из однородной системы линейных алгебраических уравнений (А - λЕ)х = 0 при λ = 1 находим собственный вектор е₁ = (1 - 1)^T . Тогда вектор e₂ = (1 1)^T , ортогональный вектору e₁, будет собственным вектором с соответствующим собственным значением λ₂ = 9 (см. 7.4). Пронормировав эти векторы, составляем из столбцов их координат матрицу ортогонального преобразования

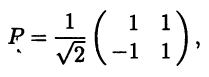
которой соответствует линейная замена переменных х = Ру. #

Единообразное поведение самосопряженных операторов и квадратичных форм при замене ортонормированного базиса объясняется следующей связью.

Теорема 8.3. Пусть А: Ε → Ε - самосопряженный oneратор, действующий в евклидовом пространстве Ε. Функция f(x) = (Аx, x), определенная на евклидовом пространстве, является квадратичной формой. Наоборот, для любой квадратичной формы f(x) на евклидовом пространстве Ε существует такой самосопряженный оператор А, что f(x) = (Аx, x). Этот оператор определен однозначно.

◄ Чтобы доказать первое утверждение теоремы, вспомним, как записывается скалярное произведение в ортонормированном базисе (см. 3.7). Используя такую запись и учитывая самосопряженность оператора, получаем

(Аx, x) = (x, Аx) = x^2TАx,

где х - столбец координат вектора x; А - матрица линейного оператора А. Мы пришли к координатной записи х^TАх некоторой квадратичной формы.

Пусть f(x) - квадратичная форма, которая в данном ортонормированном базисе е имеет вид f(x) = х^TАх. Взяв самосопряженный оператор А, который в базисе е имеет матрицу А, получаем

f(x) = х^TАх = х^T(Ах) = (x, Аx) = (Аx, x).

Наконец, докажем, что если для Двух самосопряженных операторов А и В выполняется равенство (Аx, x) = (Вx, x) для любого вектора x ∈ Ε, то А = В. Записав указанное равенство в координатах (А, В - матрицы операторов, х - столбец координат вектора x), получаем х^TАх = х^TВх, т.е. равенство двух многочленов второй степени от n переменных. Такое равенство возможно лишь в том случае, когда все коэффициенты этих многочленов при одинаковых слагаемых равны, но это эквивалентно равенству матриц А = В и, следовательно, равенству самосопряженных операторов. ►

1. Линейные операции над векторами

2. Базис. Cкалярное произведение

3. Векторное и смешанное произведения векторов

4. Декартова система координат. прямая на плоскости

5. Плоскость в пространстве

6. Прямая в пространстве

7. Кривые второго порядка — I

8. Кривые второго порядка — II

9. Поверхности второго порядка

10. Матрицы и операции с ними

11. Обратная матрица

12. Ранг матрицы

13. Системы линейных алгебраических уравнений

14. Свойства решений однородных и неоднородных СЛАУ