Приведение симметрической матрицы к диагональному виду

Матрица А линейного оператора А при замене базиса преобразуется согласно формуле А' = U^-1AU, где U - матрица перехода (см. теорему 4.6). Если речь идет об евклидовом пространстве и переходе из одного ортонормированного базиса в другой, матрица перехода U является ортогональной (см. теорему 7.5). Согласно свойству 7.2, такая матрица удовлетворяет соотношению U^-1 = U^T. Поэтому для случая ортонормиро- ванных базисов формулу преобразования матрицы линейного оператора можно записать следующим образом:

А' = U^TAU. (7.5)

Теорема 7.7. Для любой симметрической матрицы М существует такая ортогональная матрица U, что U^TMU = Λ, где Λ = diag(λ₁, ..., λ_n) - диагональная матрица, диагональными элементами которой являются собственные значения матрицы М, повторяющиеся согласно их кратности.

◄ Доказательство теоремы основано на следствии 6.4, теореме 7.5 и свойстве 7.2. Согласно следствию 6.4, для симметрической матрицы М порядка n существует такая невырожденная матрица Р, что Р^-1МР = Λ = diag(λ₁, ..., λ_n), где в последовательности λ₁, ..., λ_n указаны все собственные значения матрицы М с учетом их кратностей. Из доказательства того же следствия вытекает, что Р является матрицей перехода между ортонормированными базисами. Поэтому Р - ортогональная матрица (см. теорему 7.5) и Р^-1 = Р^T (см. свойство 7.2). Следовательно, Р^TМР = Р^-1МР = Λ, т.е. в качестве матрицы U в формулировке теоремы можно взять Р. ►

Преобразование (7.5) с ортогональной матрицей U иногда называют ортогональным преобразованием матрицы А. Поэтому теорему 7.7 можно сформулировать так: любая симметрическая матрица ортогональным преобразованием приводится к диагональному виду. Чтобы найти соответствующую матрицу U, о которой говорится в этой теореме, необходимо:

1) найти собственные значения матрицы М;

2) для каждого собственного значения найти набор собственных векторов, соответствующих этому собственному значению, при этом эти собственные векторы должны быть линейно независимыми и их количество должно равняться кратности собственного значения;

3) преобразовать системы собственных векторов, полученные для каждого собственного значения, в ортонормированные при помощи процесса ортогонализации Грама - Шмидта. Объединить ортонормированные системы для каждого собственного значения в единую систему векторов, которая будет ортонормированным базисом евклидова пространства;

4) выписать матрицу U, столбцами которой являются координаты векторов построенной ортонормированной системы.

Пример 7.4. Найдем ортогональное преобразование, приводящее симметрическую матрицу

к диагональному виду.

1. Находим собственные значения матрицы А. Для этого составляем ее характеристическое уравнение

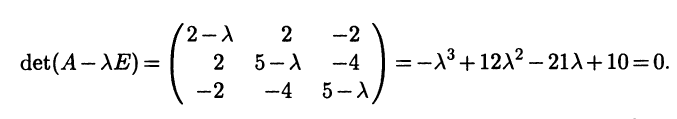
Это уравнение третьей степени. Так как его коэффициенты являются целыми числами, то целое число может быть его корнем лишь в случае, если оно делитель свободного члена. Поэтому мы можем поискать корни среди чисел ±1, ±2, ±5. Подстановкой в уравнение убеждаемся, что одним из корней является λ₁ = 1.

Найденный корень позволяет разложить левую часть харак-теристического уравнения на линейный и квадратичный мно-жители, например, при помощи деления характеристического многочлена на х - 1 "в столбик"

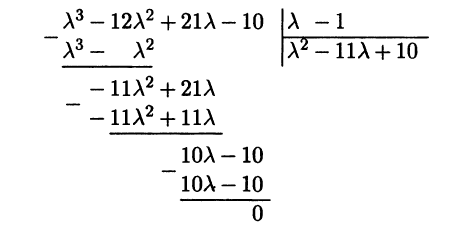
Получаем разложение

(λ - 1)(λ² - 11λ + 10) =0,

откуда находим оставшиеся два корня λ₂ = 1, λ₃ = 10. Таким образом, имеются два собственных значения: 1 кратности 2 и 10 кратности 1.

2-3. Найдем для собственного значения λ_1,2 = 1 кратности 2 два линейно независимых собственных вектора. Для этого нужно найти фундаментальную систему решений однородной системы линейных алгебраических уравнений (А - Е)х = 0, т.е. системы

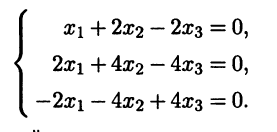
Ранг матрицы этой системы равен единице (все строки матрицы системы пропорциональны), поэтому можно отбросить второе и третье уравнения, оставив первое

х₁ + 2x₂ - 2х₃ = 0.

В качестве независимых переменных выбираем x₂, х₃. Фундаментальную систему решений составляют x₂ = 1, х₃ = 0, х₁ = - 2 и x₂ = 0, х₃ = 1, x₁ = 2, т.е. векторы

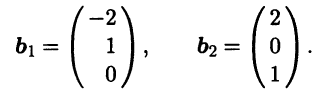
Найденные собственные векторы, соответствующие собственному значению λ_1,2 = 1, линейно независимы, но ортогональными не являются. Построим по ним другую, ортонормированную пару собственных векторов е₁, e₂ при помощи метода ортогонализации Грама - Шмидта:

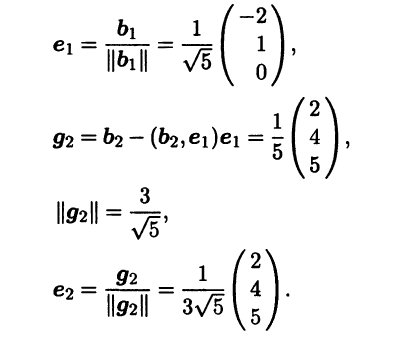
Для собственного значения λ₃ = 10 система линейных алгебраических уравнений имеет вид (А - 10Е)х = 0, или

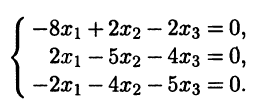
В качестве ее фундаментальной системы решений можно взять одно ненулевое решение, например вектор b₃ = (1 2 -2)^T . Нормируя этот вектор, получаем

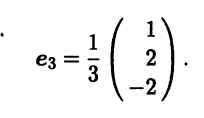
Найденные векторы e₁, е₂, е₃ образуют ортонормированный базис из собственных векторов.

4. Составим из найденных векторов е_i матрицу

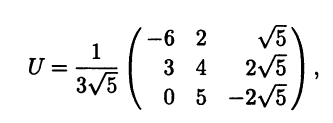
которая и является искомой.

Убедиться в том, что матрица U определена правильно, можно при помощи подстановки матрицы U и заданной матрицы А в следующее тождество:

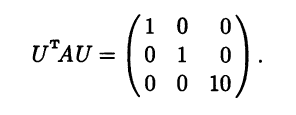
Замечание 7.4. В случае n = 3 при λ₁ = λ₂ ≠ λ₃ собственные векторы удобнее с точки зрения экономии вычислений находить в следующем порядке. Сначала для собственного значения кратности 1 (λ₃ = 10 в рассмотренном примере) найти собственный вектор и нормировать его. Обозначим полученный вектор, например, е₃. Затем для собственного значения кратности 2 (λ_1,2 = 1 в рассмотренном примере) найти один собственный вектор и нормировать его. Получим вектор e₁. Векторы е₁ и е₃ будут ортогональными согласно теореме 6.4. Недостающий третий вектор ортонормированного базиса может быть найден при помощи векторного произведения: е₂ = e₁ × е₃.

Описанный прием позволяет избежать процесса ортогона- лизации. Точно так же можно не применять процесс ортогона- лизации при n = 2, так как, зная один вектор е₁ ортонормированного базиса, мы можем получить второй поворотом первого на 90°. Для этого достаточно поменять две координаты вектора e₁ местами, а у первой из них к тому же изменить знак. При n > 3 приемов, аналогичных описанным, нет.

Вопросы и задачи

1. Опишите множество всех ортогональных матриц второго порядка.
2. Пользуясь результатами задачи 7.1, докажите, что любой ортогональный оператор в евклидовом пространстве V₂ является либо поворотом вектора на некоторый угол, либо симметрией относительно некоторой прямой, либо произведением таких операторов.
3. Докажите, что произведение ортогональных операто-ров является ортогональным оператором. Можно ли утверждать, что: а) сумма ортогональных операторов есть ортогональный оператор? б) произведение ортогонального оператора на число есть ортогональный оператор?
4. Докажите, что линейный оператор А в евклидовом пространстве тогда и только тогда является ортогональным, когда А*А = I.
5. Докажите, что если Н - инвариантное подпростран-ство для ортогонального оператора А, то и H^⊥ - тоже инвариантное подпространство этого оператора.
6. Докажите, что собственными значениями ортогонального оператора могут быть лишь числа 1 и -1.
7. Приведите пример ортогонального оператора, не имеющего собственных векторов. Какой может быть размерность евклидова пространства, в котором есть такие операторы?
8. Докажите, что любой ортогональный оператор в пространстве V₃ имеет собственный вектор. Используя результаты задач 7.2 и 7.5, опишите множество ортогональных операторов в V₃.
9. Докажите, что любому перемещению твердого тела вокруг неподвижной точки из одного положения в другое соответствует ортогональный оператор в пространстве V₃ и что эти положения связаны между собой вращением тела вокруг неподвижной оси. Эта ось проходит через неподвижную точку и параллельна собственному вектору указанного ортогонального оператора.
10. Приведите пример оператора, одновременно являющегося и самосопряженным, и ортогональным.
11. Приведите к диагональному виду ортогональным преобразованием следующие симметрические матрицы:

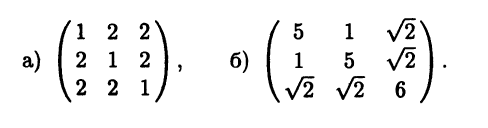
1. Линейные операции над векторами

2. Базис. Cкалярное произведение

3. Векторное и смешанное произведения векторов

4. Декартова система координат. прямая на плоскости

5. Плоскость в пространстве

6. Прямая в пространстве

7. Кривые второго порядка — I

8. Кривые второго порядка — II

9. Поверхности второго порядка

10. Матрицы и операции с ними

11. Обратная матрица

12. Ранг матрицы

13. Системы линейных алгебраических уравнений

14. Свойства решений однородных и неоднородных СЛАУ