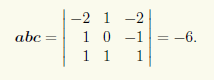Смешанное произведение

Определение 3.3. Смешанным произведением трех векторов a, b, с называют число, равное (a×b)c — скалярному произведению векторного произведения первых двух векторов и третьего вектора.

Обозначают смешанное произведение трех векторов a, b, с так: abc.

Смешанное произведение имеет простой геометрический смысл.

Теорема 3.1. Смешанное произведение трех некомпланарных векторов abc равно объему параллелепипеда, построенного на этих векторах как на ребрах, выходящих из одной вершины, взятого со знаком плюс, если тройка векторов a, b, с — правая, и со знаком минус, если эта тройка — левая.

◄ Вектор a×b перпендикулярен грани указанного параллелепипеда, построенной на векторах a и b, и в силу свойства 2° векторного произведения имеет длину, равную площади S этой грани (рис. 3.6). Обозначив через e единичный вектор, ортогональный векторам a и b и однонаправленный с векторным произведением a×b, получим

a×b = Se.

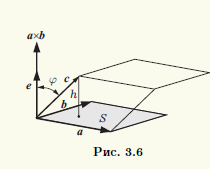
Смешанное произведение abc равно скалярному произведению вектора Se на вектор с и равно S |c| cosφ, где φ — угол между векторами a×b и c. Отметим, что число |c| cosφ равно проекции вектора c на направление вектора е, а его модуль, т.е. ||c| cosφ|, равен высоте h параллелепипеда. Знак проекции определяется углом φ между c и е. Если φ < 90°, то векторы c и е находятся по одну сторону от плоскости векторов a, b. Значит, тройки векторов a, b, е

и a, b, c имеют одну и ту же ориентацию — правую. В этом случае смешанное произведение положительно и равно объему параллелепипеда со знаком плюс. Если же φ > 90°, то ориентация указанных троек различная, т.е. тройка a, b, c является левой, и смешанное произведение будет равно объему параллелепипеда со знаком минус. Отметим, что равенство φ = 90° невозможно, так как оно означает, что вектор c находится в плоскости векторов a и b, а это противоречит условию некомпланарности этих векторов. ►

Замечание 3.2. Если векторы a, b, c компланарны, то параллелепипед, построенный на них, вырождается (лежит в плоскости). Поэтому ему следует приписать нулевой объем. Непосредственно из определения заключаем, что для компланарных векторов a, b, c векторы a×b и c ортогональны, т.е. (a×b)c = 0. Значит, теорема верна и в случае, когда векторы компланарны. #

Свойства смешанного произведения.

1°. Для смешанного произведения действует правило циклической перестановки:

abc = bca = cab = —bac = —cba = —acb.

◄ Действительно, все шесть указанных произведений по абсолютной величине дают объем одного и того же параллелепипеда, а знак произведений определяется ориентацией тройки сомножителей. При циклической перестановке векторов в тройке ориентация не меняется, при перестановке местами двух векторов в тройке ориентация меняется на противоположную. ►

Замечание 3.3. Из доказанного свойства получаем, что

abc = (a×b)c = a(b×c),

т.е. порядок двух операций, дающих смешанное произведение, не является существенным. Это объясняет, почему в обозначении смешанного произведения знаки образующих операций опускаются.

2°. Три вектора a, b, c компланарны тогда и только тогда, когда их смешанное произведение равно нулю.

◄ Это вытекает из теоремы 3.1 и замечания 3.2. ►

3°. Для смешанного произведения выполняется свойство ассоциативности относительно умножения векторов на число: (λa)bc = λ(abc).

◄ Обозначив b×c = e и используя свойство 2° ассоциативности скалярного произведения относительно умножения на число, получим

(λa)bc = (λa)(b×c) = (λa)e = λ(aе) = λ(a(b×c)) = λabc. ►

4°. Для смешанного произведения выполняется свойство дистрибутивности (a₁ + a₂)bc = a₁bc + a₂bc.

Обозначив b×c = e и используя свойство 3° дистрибутивности скалярного произведения, получим

(a₁ + a₂)bc = (a₁ + a₂)(b×c) = (a₁ + a₂)e = a₁e + a₂e = a₁(b×c) + a₂(b×c) = a₁bc + a₂bc. ►

Замечание 3.4. Свойства 3° и 4° смешанного произведения сформулированы для первого сомножителя. Однако при помощи циклической перестановки можно доказать аналогичные утверждения и для второго и для третьего сомножителей, т.е. верны равенства

a(λb)c = λ(abc), ab(λc) = λ(abc), a(b₁ + b₂)c = ab₁c + ab₂c, ab(c₁ + c₂) = abc₁ + abc₂,

и в итоге имеем свойство линейности смешанного произведения по каждому сомножителю.

Замечание 3.5. Отметим, что при доказательстве свойств смешанного произведения мы не использовали свойства векторного произведения. Наоборот, обоснование свойств векторного произведения можно строить на основе свойств смешанного произведения. Покажем это на примере свойства дистрибутивности векторного произведения, доказательство которого мы обещали привести.

Сначала обратим внимание на следующее. Если векторы х₁ и х₂ таковы, что для любого вектора у выполняется равенство

x₁y = x₂у, (3.3)

то х₁ = х₂. Действительно, равенство (3.3) означает, что (х₁ — х₂)у = 0. Так как вектор у любой, мы можем положить у = х₁ — х₂. Тогда получим (х₁ — х₂)² = 0, но это возможно только при х₁ — х₂ = 0, т.е. при х₁ = х₂.

Согласно доказанному, равенство

(а₁ + а₂)×b = а₁×b + а₂×b

будет выполняться, если для любого вектора с

((а₁ + a₂)×b)c = (a₁×b)c + (a₂×b)c,

или

(а₁ + a₂)bc — a₁bc + a₂bc.

Но последнее равенство верно, так как выражает доказанное свойство 4° дистрибутивности для смешанного произведения. #

Пусть векторы a, b, c заданы своими координатами в правом ортонормированном базисе: a = {x_a; y_a; z_a}, b = {x_b; y_b; z_b}, c = {x_c; y_c; z_c}. Чтобы найти их смешанное произведение, воспользуемся формулами для вычисления скалярного и векторного произведений:

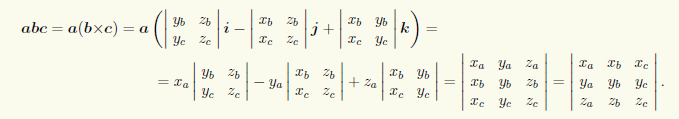
Согласно полученной формуле, свойство 2° смешанного произведения можно сформулировать так: необходимым и достаточным условием компланарности трех векторов, заданных координатами в ортонормированном базисе, является равенство нулю определителя третьего порядка, строками которого являются координаты этих векторов.

Пример 3.3. Найдем объем треугольной пирамиды, построенной на векторах

a = {—2;1; -2}, b = {1;0; —1}, c = {1; 1;1}

как на смежных ребрах.

Трем векторам с общим началом можно сопоставить как треугольную пирамиду, так и параллелепипед, причем объем пирамиды будет в 6 раз меньше объема параллелепипеда, равного модулю смешанного произведения abc данных векторов. Итак, объем пирамиды равен V = |abc|/6 = 1, поскольку